Question

Решите пожалуйста!!!! Знайдіть площу прямокутної трапеції , гострий кут якої дорівнює 30 градусів, а висота-6см,якщо в цю трапецію можна вписати коло.

Answer 1

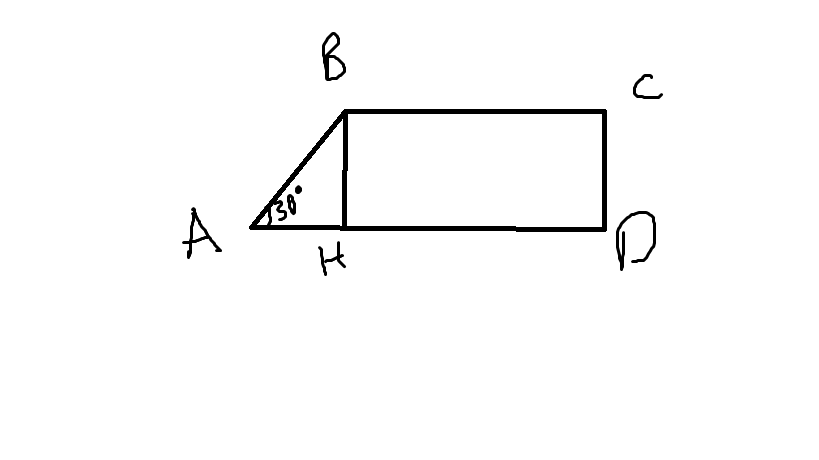
Треугольник ABH:

AB=2*BH=2*6=12(против угла в 30 градусов лежит кактет равный половине гипотенузы)

cos30=AH/AB

$AH=cos30*AB=12*frac{sqrt{3}}{2})=6sqrt{3}$

HD=BC(т.к. прямоугльник) 

AD=AH+HD=AH+BC 

Если в трапецию можно вписать окружность, то сумма противоположных сторон равны:

AB+CD=BC+AD

$12+6=BC+(AH+BC)\18-6sqrt{3}=2BC\9-3sqrt{3}=BC\AD=(9-3sqrt{3})+6sqrt{3}=9+3sqrt{3}$

$S=frac{BC+AD}{2}*h =frac{9-3sqrt{3}+ 9+3sqrt{3}}{2}*6=frac{18}{2}*6=54$

Answer 2

Если трапеция прямоугольная, значит высота равна боковой стороне. Одна боковаыя сторона равна 6, а другая - в два раза больше (так как синус противолежащего угла равен 30 градусов), т.е. 12.

Если в трапецию можно вписать окружность, то сумма ее оснований равна сумме боковых сторон. Значит, сумма оснований данной трапеции равна 6 + 12 = 18.

Полусумма оснований равна 18/2 = 9.

Площадь трапеции равна произведению полусуммы оснований на высоту, т.е. 9*6 = 54 кв. см.

 

Ответ: 54 кв. см.