Предмет: Математика,
автор: PigWin4ester
Частная производная функции z=e^(x^2+y^2) по переменной x в точке М (-1;1) равна?
Желательно подробно.
Ответы
Автор ответа:
0
Решение на фото.
При дифференцировании следуем правилу дифференцированию сложной функции: производная экспоненты — сама экспонента, после чего нужно умножить на производную показателя (x^2+y^2) по х, а это будет 2х.
Далее просто подставляем имеющиеся значения х и у.
При дифференцировании следуем правилу дифференцированию сложной функции: производная экспоненты — сама экспонента, после чего нужно умножить на производную показателя (x^2+y^2) по х, а это будет 2х.
Далее просто подставляем имеющиеся значения х и у.
Приложения:
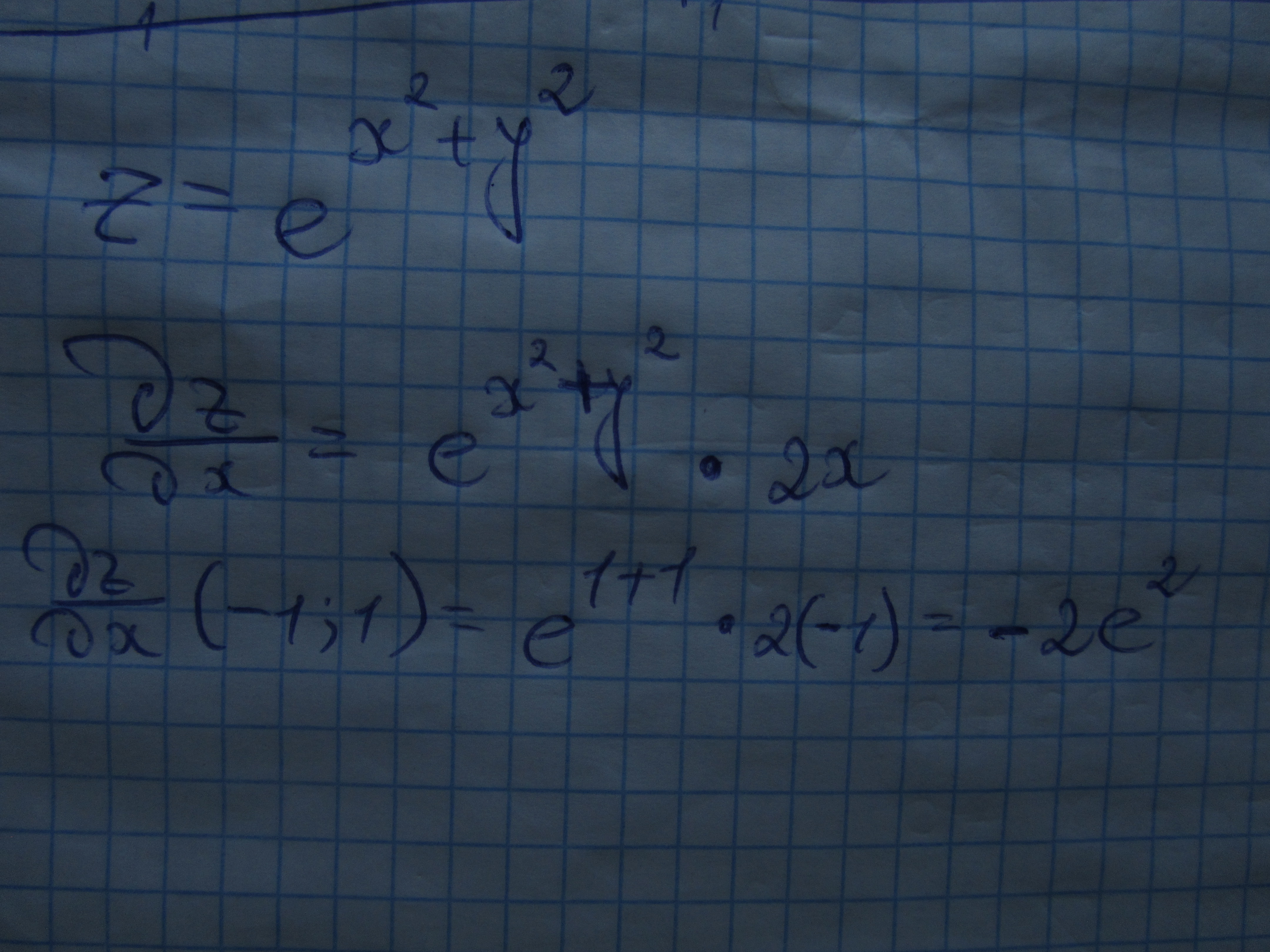
Автор ответа:
0
При дифференцировании (x^2+y^2) по х мы дифференцируем отдельно каждое слагаемое. Производная x^2 равна 2x (табличное значение), а вот производная y^2 будет равна нулю, так как дифференцирование по иксу (в этом случае y^2 считается просто константой).
Автор ответа:
0
Все теперь понял. Спасибо.
Похожие вопросы
Предмет: Математика,
автор: sisenbaialmat
Предмет: Алгебра,
автор: Denelogik
Предмет: Химия,
автор: ososos82
Предмет: Алгебра,
автор: vitek6
Предмет: Алгебра,
автор: Acaciadealbat