Предмет: Алгебра,
автор: Limon4ic228
Существуют ли выпуклые 12-угольник, который можно разделить на конечное число квадратов и равносторонних треугольников? ответ обоснуйте/
Ответы
Автор ответа:
0
Не буду рассказывать, как я до этого доходил, но доказывается построением, как и всегда, когда хочется доказать существование.
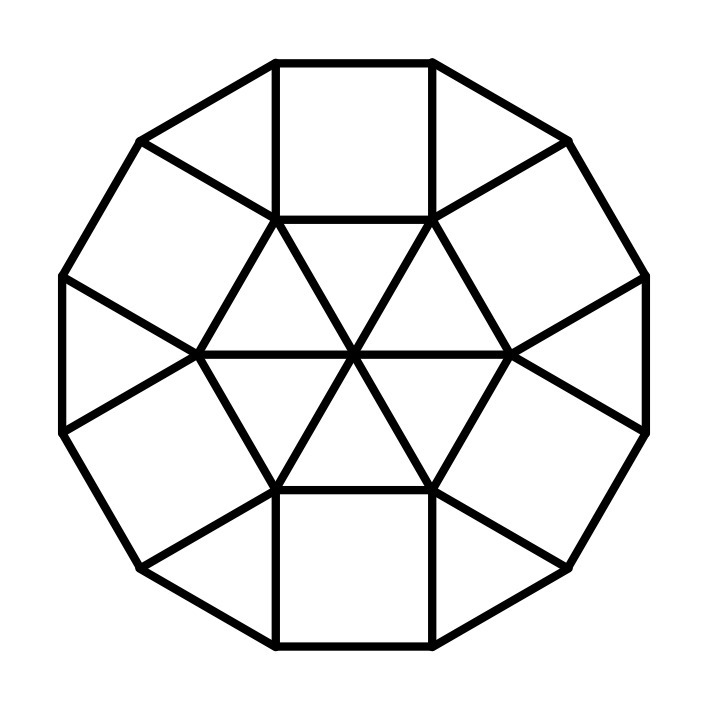
Берем правильный 12-ти угольник, внешнее кольцо выкладываем из чередующихся квадратов и треугольников (сумма их углов при вершинах равна 150, как раз углу правильного 12-ти угольника). Оставшийся внутренний правильный шестиугольник выкладываем треугольниками.
Смотри приложение
Берем правильный 12-ти угольник, внешнее кольцо выкладываем из чередующихся квадратов и треугольников (сумма их углов при вершинах равна 150, как раз углу правильного 12-ти угольника). Оставшийся внутренний правильный шестиугольник выкладываем треугольниками.
Смотри приложение
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: muratzanadilbekov
Предмет: Математика,
автор: boichenko730
Предмет: Информатика,
автор: EzGLA
Предмет: Литература,
автор: posohoffroman2
Предмет: История,
автор: mongontuya