Question

В выпуклом четырёхугольнике KLMN сторона LM меньше стороны KN. Обозначим середины сторон KL и MN через X и Y соответственно. Известно, что прямые KN и LM пересекают продолжение YX в точках V и W соответственно. Докажите, что угол KVX меньше угла LWX.

Answer 1

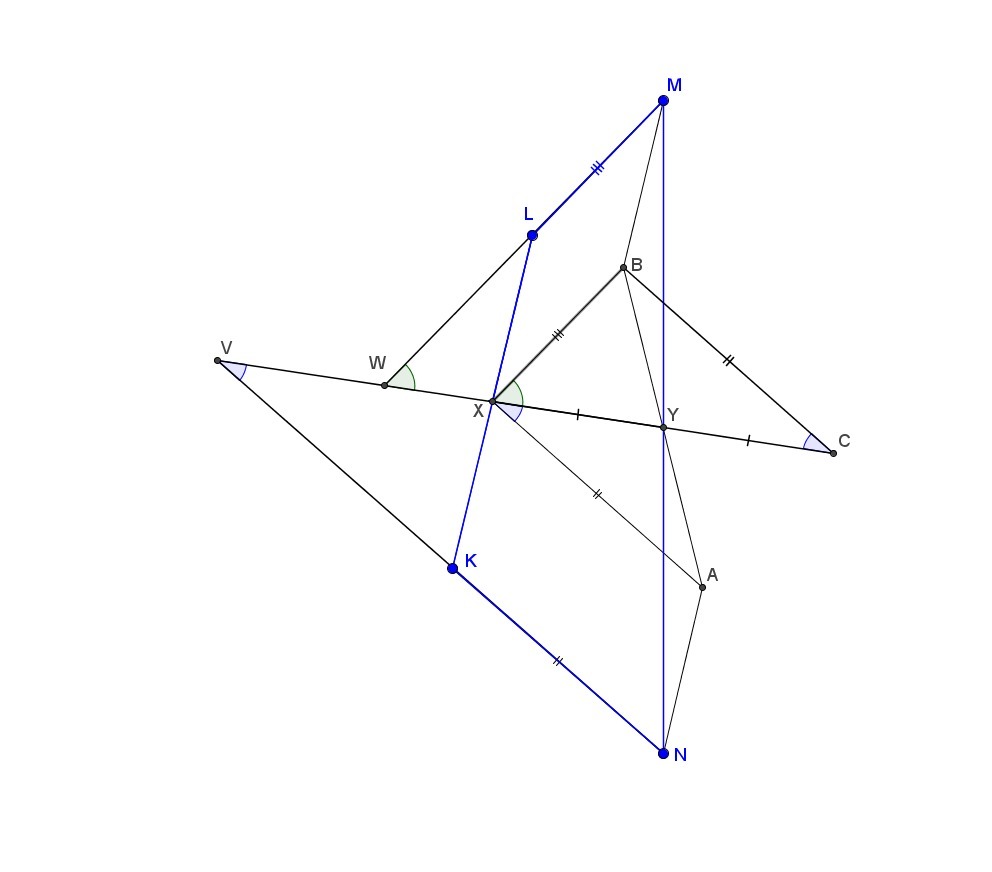
Возьмем точки А и В так, чтобы XKNA и XLMB были параллелограммами и продлим XY за точку Y на свою длину до точки С (см. рис). Треугольник ANY равен треугольнику BMY по двум сторонам и углу между ними (AN=XK=XL=BM, NY=MY и ∠ANY=∠BMY как внутренние накрест лежащие, т.к. АN||KL||MB и MN - секущая). Значит AY=BY, т.е. AXBC - параллелограмм. Тогда ∠KVX=∠AXY=∠XCB, ∠LWX=∠BXC, BC=XA=KN и BX=LM, а т.к. по условию LM<KN, то BX<BС. Т.к. в любом треугольнике (в том числе XCB) напротив меньшей стороны лежит меньший угол, то ∠XCB<∠BXC, а значит и ∠KVX<∠LWX.