2. Решите задачу.
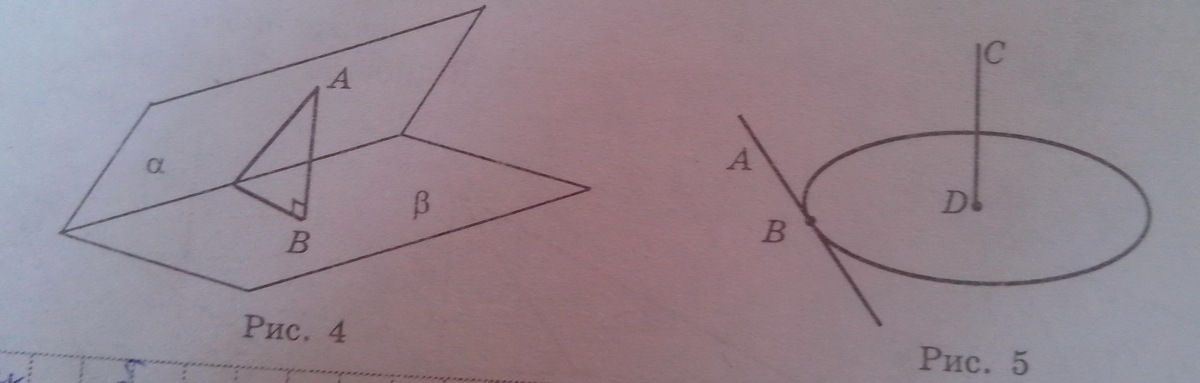
а) * На одной из граней двугранного угла взята точка (рис. 4). Найдите расстояние от данной точки до ребра угла, если точка удалена от второй грани на 6 см, а градусная мера двугранного угла равна 60 °.
б) * На одной из граней двугранного угла обозначено точку (рис. 4). Найдите расстояние от данной точки до второй грани, если точка удалена от ребра угла на 10 см, а градусная мера двугранного угла равна 30 °.
в) ** На рис. 5 АВ - касательная к окружности с центром D, CD перпендикулярно (ABD) Найдите
угол между плоскостями АВС и АВD, если CD = 4 см, а площадь круга, ограниченного данным кругом, составляет 9 pi см²
г) *** Угол между плоскостями равнобедрених треугольников АВС и ABD которые имеют общую основу АВ, равна 60 °. Найдите СD, если АВ = 48 см, ВС = 30 см, ВD = 26 см.
Ответы
1) то есть 6/sin60=x/sin90
x=4V3
теперь найдем длину искомую
d=(4V3)^2+6^2= V48+36=2V21
2) 10/sin90=x/sin30
2x=10
x=5
3) тогда радус кргу равен
S=pir^2=9pi
R=3
ВД=3
ДС=4
Рассмотрим треугольник он прямоугольный гипотнуза равна 3^2+4^2=5^2
то есть 5
возьмем гип ВС=5
по теореме , косинусов
4^2 = 5^2+3^2-2*15*cosa
cosa=3/5
a=arcsin(3/5)
4) ОВ=48/2 = 24
ОС= V30^2-24^2=18
OD= V26^ 2-24^ 2 = 10
угол еще
x=V18^2+10^2-2*180*cos60= 2V61