Предмет: Алгебра,
автор: севак12
помогите завтра в школу
Приложения:
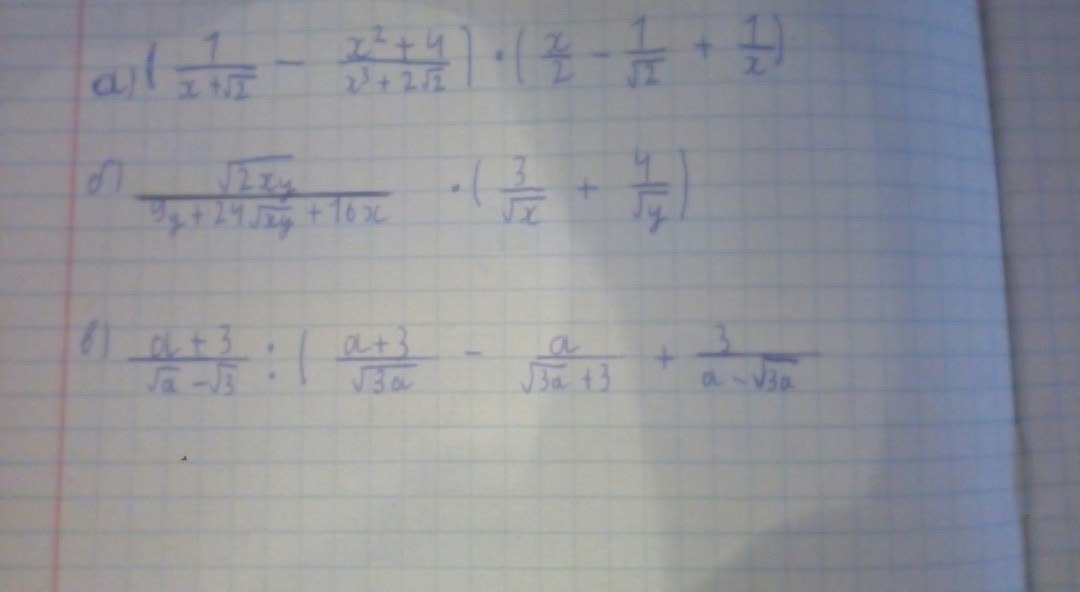
Ответы
Автор ответа:
0
a)



б)



в)




б)
в)
Похожие вопросы
Предмет: Математика,
автор: olegVek
Предмет: Математика,
автор: zdemidenko70
Предмет: История,
автор: maundurovgaidar
Предмет: Математика,
автор: farida197767