Предмет: Геометрия,
автор: ruveh
В равнобедренной трапеции основания равны 6см и 10 см
а диагональ равна 17 см найти площадь трапеции
Ответы
Автор ответа:
0
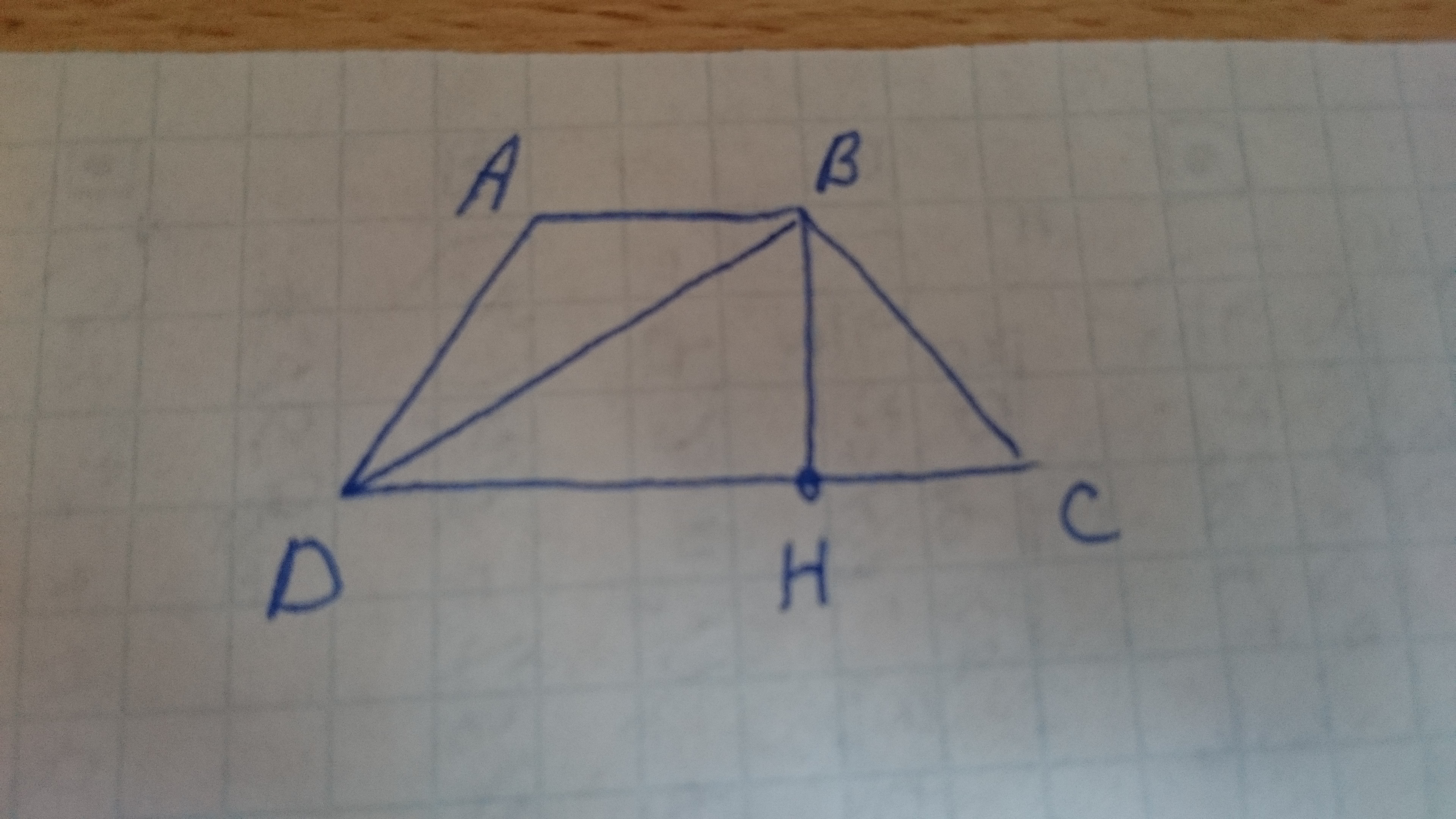
AB = 6 см
DC = 10 см
BD = 17 см
BH - высота.
HC = (DC-AB)/2 = (10-6)/2 = 2 см
DH = DC-HC = 10-2 = 8 см
Из ΔBHD по теореме Пифагора находим BH:
BH = √(BD²-DH²) = √(289-64) = √225 = 15 см
S трапеции = (a+b)/2 * h = (AB+DC)/2 * BH = (6+10)/2 * 15 = 120 см²
DC = 10 см
BD = 17 см
BH - высота.
HC = (DC-AB)/2 = (10-6)/2 = 2 см
DH = DC-HC = 10-2 = 8 см
Из ΔBHD по теореме Пифагора находим BH:
BH = √(BD²-DH²) = √(289-64) = √225 = 15 см
S трапеции = (a+b)/2 * h = (AB+DC)/2 * BH = (6+10)/2 * 15 = 120 см²
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: dkruckov17
Предмет: Окружающий мир,
автор: yulyapak127
Предмет: Математика,
автор: katerinicaleksandra5
Предмет: Информатика,
автор: aaaa622
Предмет: Алгебра,
автор: gun85