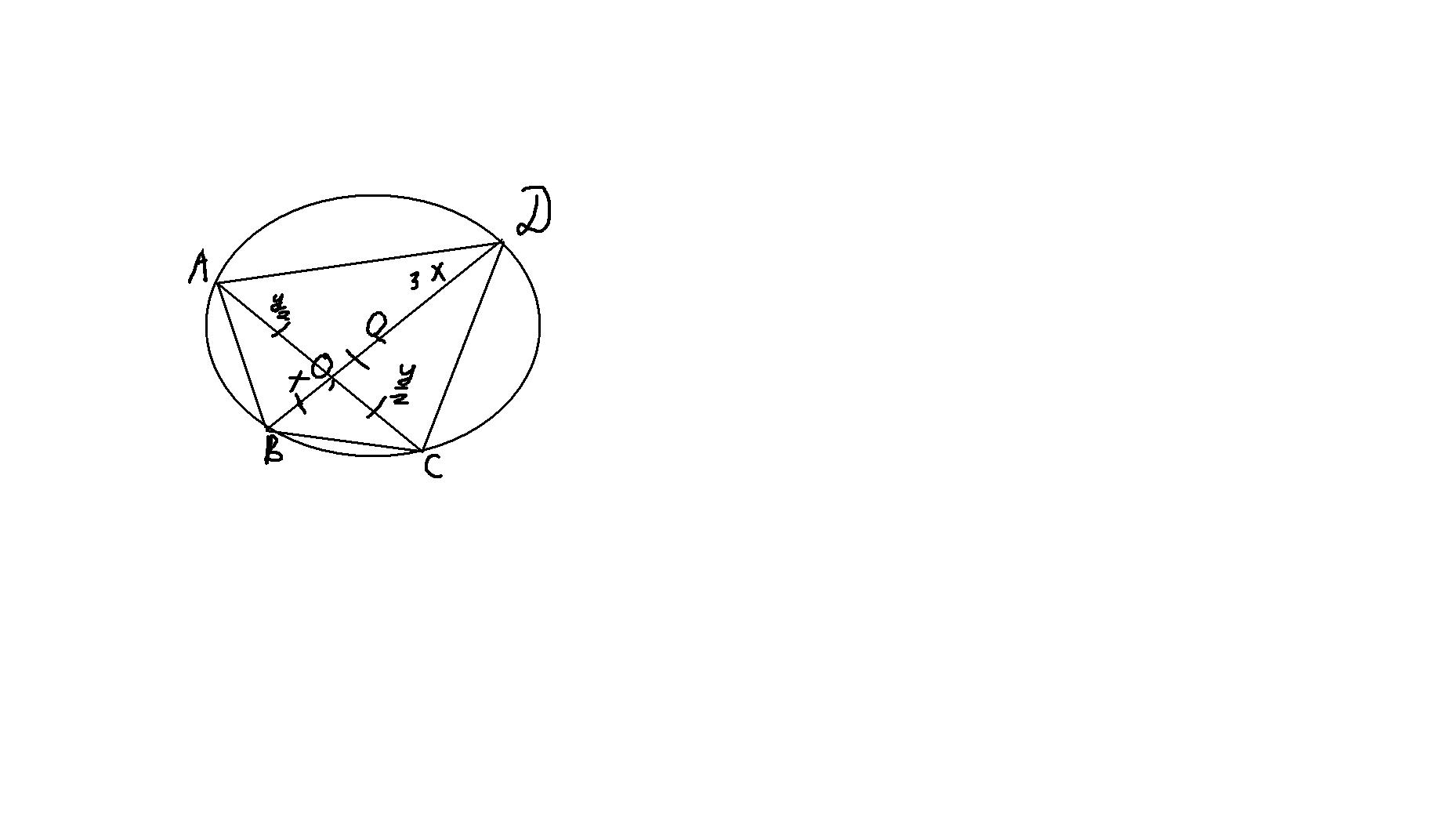
номер 1 Отрезок ВД диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСД и градустные муры дуг АВ ВС СД АД номер 2 Высота проведенная к основанию равнобедренного треугольника равна 9см , а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей
Ответы
1)Для начал сами углы этого четырехугольника
Обозначим точку пересечения как О1, тогда если обозначит ВО1=х следует что О1Д=3х
так как радиус равен R=D/2
При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
Тогда x*3x=y/2*y/2
3x^2=y^2/4
y=V12x где V-кв корень
y/2=V12*x/2
значит получим равнобедренный треугольник АСД рассмотрим его , по теореме Пифагора найдем АД=V9x^2+12x^2/4=V48x^2/4=4xV3/2=2xV3
теперь по теореме косинусов найдем сам угол АДС ,
AC^2=AD^2+DC^2-2*AD*DC*cosa
12x^2=12x^2*2-2*12x^2*cosa
12x^2-24x^2 = -24x^2*cosa
-12x^2/-24x^2=cosa
cos=1/2
a=60гр то есть угол АДС равен 60 гр
теперь другие
ABC угол равен
12x^2=8x^2-8x^2*cosa
-4x^2/8x^2=cosa
cosa=-1/2
a=120гр
ABC = AOC = 120 (Ромб)
Потому что вписанный угол в 2 раза меньше центрального на той же хорде AC.
BAD = BCD = 90, потому что они опираются на диаметр.
И окончательно ответ
Градусные меры дуг
AB = BC = 60
CD = AD = 120
2)
найдем сначала стороны по Пифагору
24/2=12
12^2+9^2=15^2
теперь угол
15^2=15^2+24^2-2*15*24*cosa
sina=3/5
По теореме синусов
15/3/5=2R
R=12.5
теперь вписанную
по формуле r=b/2*V(2a-b )/ (2a+b) = 12V(30-24)/(30+24)) =12V6/54=12*1/3=4см
Ответ R=12.5 r=4см