Предмет: Математика,
автор: JJJJJOOOHH
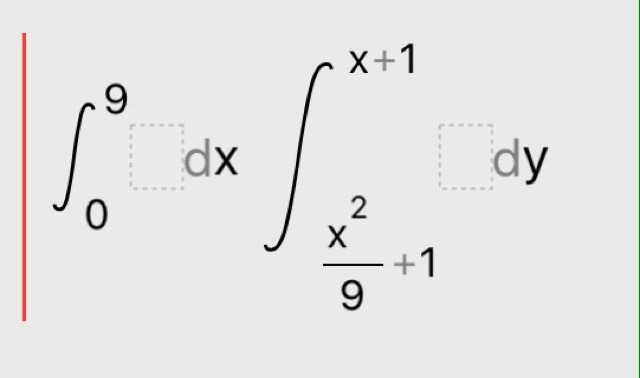
Найти площадь, поменяв пределы интернирования
Приложения:
Ответы
Автор ответа:
0
Меняем пределы интегрирования
при х=0 у=1
при х=9 у=10
1≤у≤10;
у=х+1 ⇒
х=у-1
у=(х²/9)+1 ⇒
х²=9(у-1)
y-1≤x≤3√(y-1)
=13,5
Похожие вопросы