Предмет: Алгебра,
автор: Nelli1995
Будьте добры! Помогите решить неопределенный интеграл. Буду очень благодарна!
Приложения:
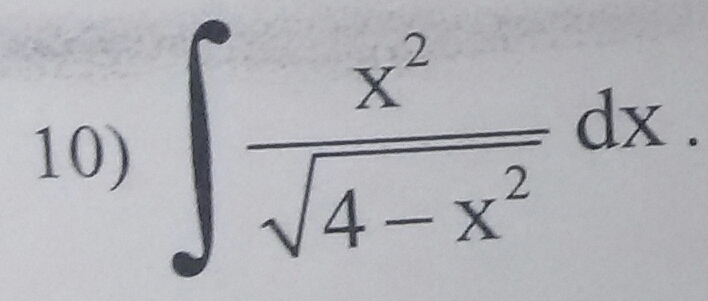
Ответы
Автор ответа:
0
Сначала делаем так:

С первым интегралом все просто, он табличный и равен
Второй интеграл будем брать по частям:

Тогда исходный интеграл равен:

Делаем следующее:

Это ответ.
С первым интегралом все просто, он табличный и равен
Второй интеграл будем брать по частям:
Тогда исходный интеграл равен:
Делаем следующее:
Это ответ.
Похожие вопросы
Предмет: Английский язык,
автор: glebg3029
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: alinasweetuzb
Предмет: Геометрия,
автор: Елена0112