Предмет: Алгебра,
автор: DHAcity
Задания простенькие поэтому по 2 номера.Ниже в коментариях(ссылка) на еще 2 таких же задания.
Решить не просто дав ответ----->ПРИМЕР ((Корень 49*81=63))
А решить нормально то есть вот так------>ПРИМЕР ((Корень 49*81=49*81=корень 3969=63))
Приложения:
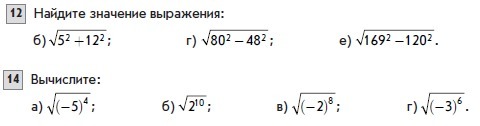
Ответы
Автор ответа:
0
№12



№14




№14
Автор ответа:
0
Можно воспользоваться формулой с модулем: корень(a^2)=|a| ---> корень( ((-3)^3)^2)= | (-3)^3 | = | -27 |=27
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: ksenyakoroleva666
Предмет: Химия,
автор: marinap10052007
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: gorynich
Предмет: Математика,
автор: maksimka1001200