при каких а ровно один корень уравнения x^2 - (2 a + 1) x - a + 6 = 0 принадлежит отрезку [0;4]?
Ответы
x² - (2 a + 1) x - a + 6 = 0
х²-2ах-х-а+6=0
х²-х+6=а·(2х+1)
а=(х²-х+6)/(2x+1)
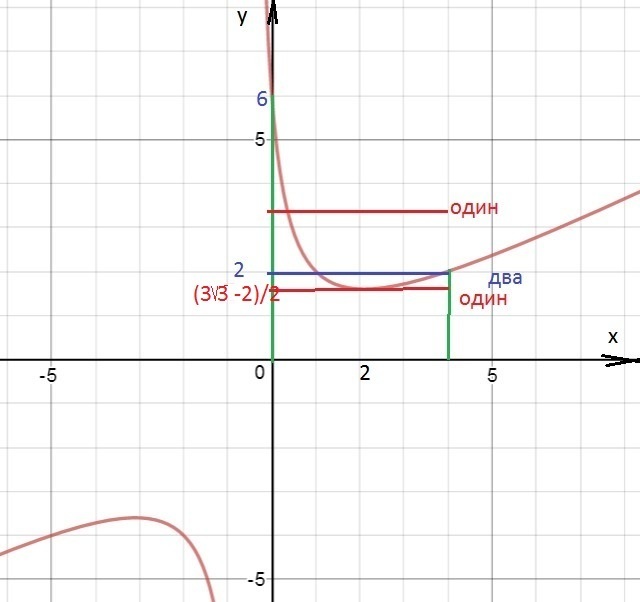
Строим график функции у=(х²-х+6)/(2x+1) и прямой у=а
(см. рисунок)
Функция у=(х²-х+6)/(2x+1) определена при х∈(-∞;-1/2)U(-1/2;+∞).
y`=((2x-1)·(2x+1)-2·(x²-x+6))/(2x+1)²
y`=0
2x²+2x-13=0
x=-1± (3√3/2)
x=-1- (3√3/2)∉[0;4]; x= -1+ (3√3/2)∈[0;4]
Найдем а, соответствующее х=-1+ (3√3/2)
а=((-1+(3√3/2))²-(-1+(3√3/2))+6)/3√3
а=(3√3-2)/2
О т в е т. при а=(3√3-2)/2 и 2<a≤6.
Второй способ.
1) Если дискриминант квадратного уравнения равен 0, то уравнение имеет один корень.
D=(2a+1)²-4·(-a+6)=4a²+8a-23
a=(-8±12√3)/8
При а=(-2-3√3)/2 уравнение имеет корень х=(-1-3√3)/2∉[0;4]
При а=(-2+3√3)/2 уравнение имеет корень х=(-1+3√3)/2∈[0;4]
2) Если дискриминант квадратного трехчлена положителен, то уравнение имеет два корня x₁ и x₂ ( х₁<x₂)
Для выполнения условия задачи, потребуем, чтобы х₁∈(0;4), х₂∉(0;4)
или х₂∈(0;4), х₁∉(0;4).
Это условие требует выполнения совокупности двух систем неравенств:
{f(0)<0
{f(4)>0
или
{f(0)>0
{f(4)<0
что равносильно неравенству f(0)·f(4)<0
f(x)=x²-(2a+1)x-a+6
(-a+6)·(18-9a)<0⇒ a∈(2;6)
При х=0 получаем, что a=6
При а=6 уравнение имеет вид х²-13х=0 и х=0 - единственный корень, принадлежащий отрезку [0;4]
При а=2 уравнение имеет вид х²-5х+4=0 уравнение имеет два корня х=1 и х=4, принадлежащих отрезку [0;4]
О т в е т. а∈{(3√3-2)/2}U(2;6].