ПОМОГИТЕ ПОЖАЛУЙСТА! УМИРАЮ! Не могу решить!
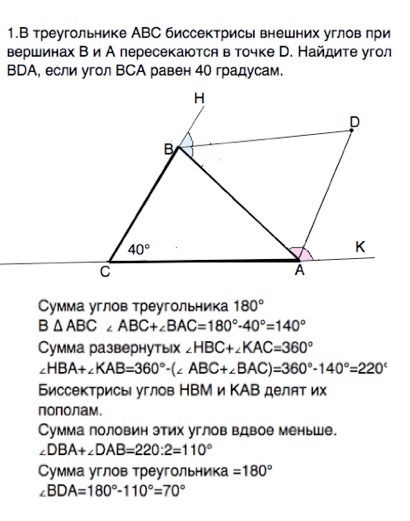
1.В треугольнике АВС биссектрисы внешних углов при вершинах В и А пересекаются в точке D. Найдите угол BDA, если угол ВСА равен 40 градусам.
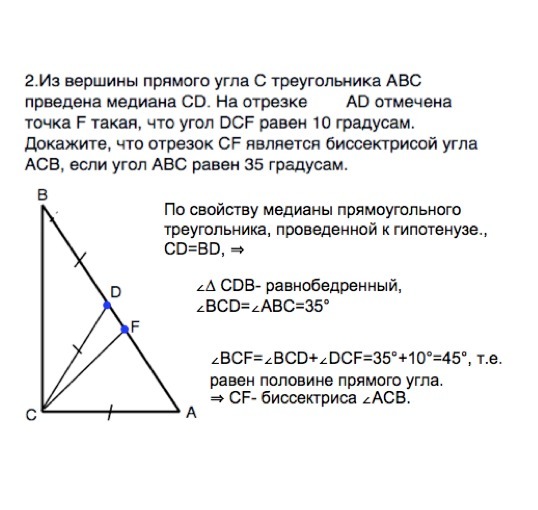
2.Из вершины прямого угла С треугольника АВС прведена медиана СD. На отрезке АD отмечена точка F такая, что угол DCF равен 10 градусам. Докажите, что отрезок СF является биссектрисой угла ACB, если угол ABC равен 35 градусам.
3.В треугольнике АВС серединный перпендикуляр к стороне АВ пересекает сторону АС в точке D. Докажите, что AC>CB.
Ответы
1) Сумма углов треугольника 180°
В ∆ АВС ∠ АВС+∠ВАС=180°- 40°=140°
Сумма развернутых углов ∠НВС+∠КАС=360°
∠НВА+∠КАВ=360°- (∠ АВС+∠ВАС)=360°-140°=220°
Биссектрисы углов НВМ и КАВ делят их пополам.
Сумма половин этих углов вдвое меньше.
∠DBA+∠DAB=220:2=110°
∠BDA=180°-110°=70°
2)
По свойству медианы прямоугольного треугольника, проведенной к гипотенузе., CD=BD, ⇒
∠∆ CDB- равнобедренный, ∠ВСD=∠ABC=35°
∠ВСF=∠BCD+∠DCF=35°+10°=45°, т.е. равен половине прямого угла.
⇒ CF- биссектриса ∠АСВ.
3)
Срединный перпендикуляр делит АВ на равные отрезки АН=ВН
∆ АDВ - равнобедренный ( DH медиана и высота).
АС=AD+DC
В треугольнике любая сторона меньше суммы двух других ( по т. о неравенстве треугольника).
В ∆ ВDС сторона ВС < ВD+DC, а BD=AD. ⇒ ВС < AD+DC
Следовательно, ВС меньше АС.