Докажите что прямые или отрезки на этих рисунках параллельны. Сделайте пожалуйста качественно!
Ответы
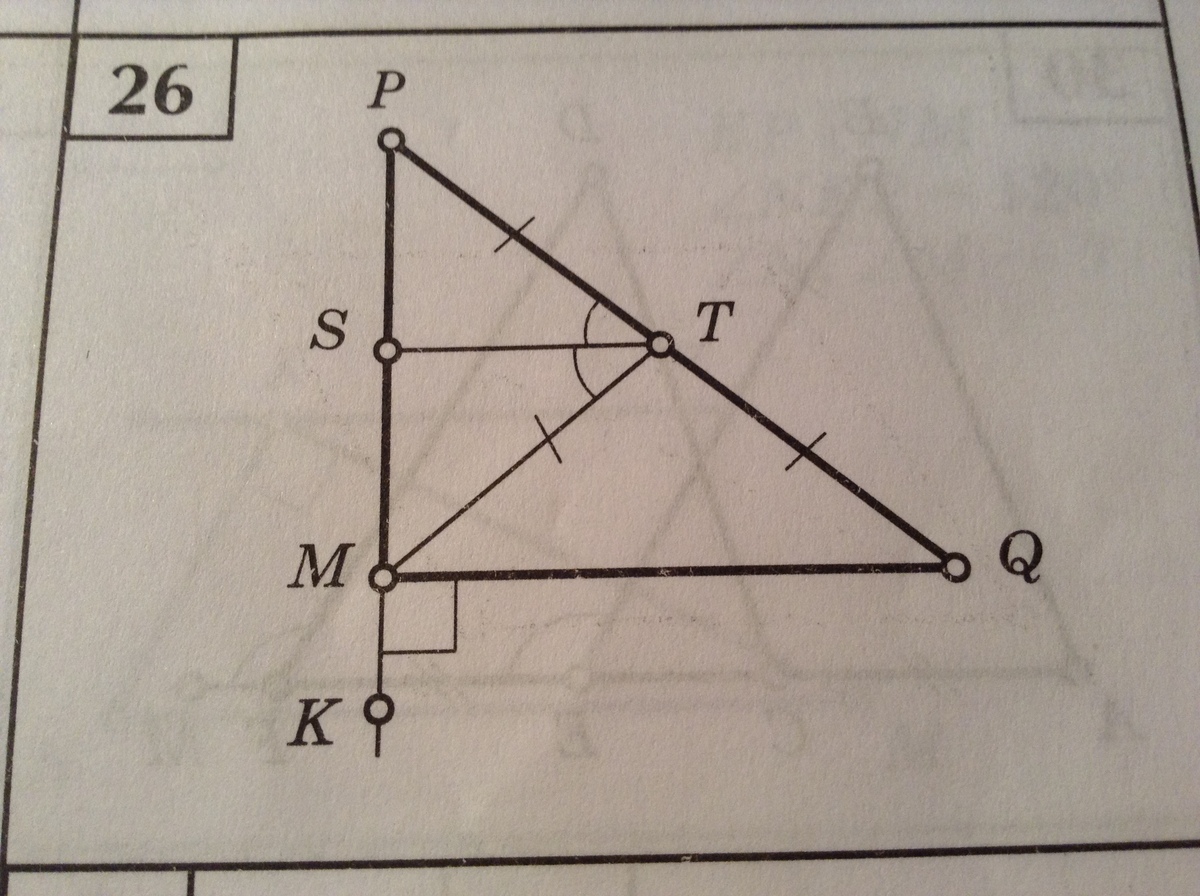
рис 26 6 треугольник PTM равнобедренный так как у него две стороны равны по условию. , следовательно биссектриса ТS является также медианой ( биссектриса , проведённая к основанию, яляется медианой и высотой в равнобедренном треугольнике) , значит S - середина РМ , Т середина РG по условию, получаем , что ST- средняя линия треугольника МРG, а она параллельна противоположной стороне , значит ST параллельна МG
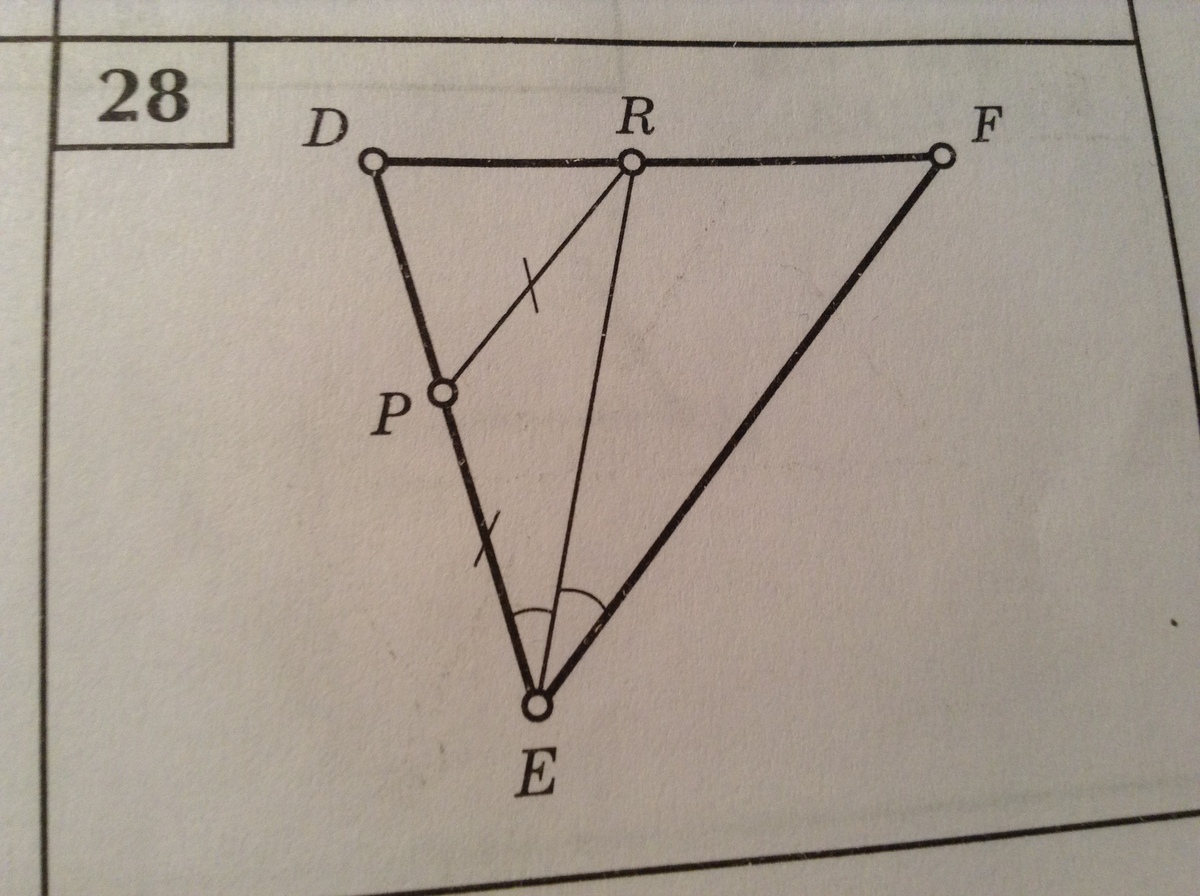
рис 28 Треугольник ЕРR равнобедренный , значит угол РЕR =углу PRE углы при основании, угол РЕR =углу RЕF по условию, значит угол PRE= углу REF , а эти углы накрест лежащие при прямых РR и EF и секущей ЕR , значит РR параллельна EF
Если нужно доказать, что на первом рисунке ST параллельно MQ, а на втором PR параллельно EF . ТО решение будет выглядеть так
1 рисунок: Раз треугольник PTM равнобедреный( PT = TM), а ST - биссектриса, то ST будет и высотой (в равнобедреном треугольнике биссектриса проведенная к основе будет являтся высотой), значит угол TSM = 90 градусов.Раз угол KMQ = углу TSM = 90 градусов (соответственные углы), то делаем вывод, что ST параллельно MQ ( 2 прямые параллельные если соответственные углы образованные при их пересечении третей прямой равны)
2 рисунок: Раз треугольник PRE равнобедренный (PR = PE), то угол PER =углу PRE (углы при основе). Угол PER=углу REF (по условию), то угол PRE= углу REF.
Раз угол PRE= углу REF, то делаем вывод, что PR параллельно EF ( угол PRE и угол REF, накрест лежащие и равные).