Предмет: Физика,
автор: Macintosh4
Помогите решить задачу очень срочно!
Приложения:
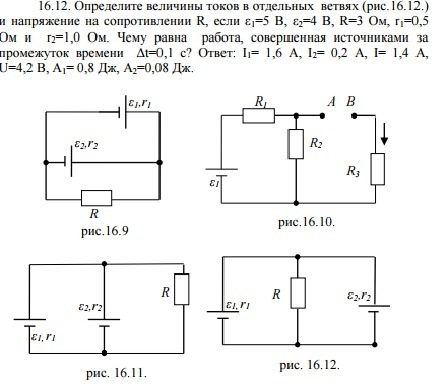
Ответы
Автор ответа:
0
Будемъ подразумѣвать токъ, идущій черезъ первый источникъ электричества въ направленіи ЭДС, какъ 
а черезъ второй, какъ: изъ чего воспослѣдуетъ, что:
изъ чего воспослѣдуетъ, что:

Изъ перваго равенства приведённаго уравненія:
 [1]
[1]
Изъ втораго равенства этого жъ уравненія:
 [2]
[2]
Раздѣлимъ [2] на [1] :





 [3]
[3]
Изъ симметріи, помѣнявъ индексы,
для втораго тока совсѣмъ нетрудно получить слѣдующее:
 [4]
[4]
Совсѣмъ несложно понять, что два послѣдніе выраженія въ суммѣ –
– это полный токъ въ нагрузкѣ:

 А ;
А ;
Измѣнимъ выраженія [3] и [4] такъ, чтобъ число подмѣнъ при послѣдующемъ счетѣ стало наименьшимъ:
 А ;
А ;
 А ;
А ;
 В ;
В ;
 Дж ;
Дж ;
 Дж .
Дж .
а черезъ второй, какъ:
Изъ перваго равенства приведённаго уравненія:
Изъ втораго равенства этого жъ уравненія:
Раздѣлимъ [2] на [1] :
Изъ симметріи, помѣнявъ индексы,
для втораго тока совсѣмъ нетрудно получить слѣдующее:
Совсѣмъ несложно понять, что два послѣдніе выраженія въ суммѣ –
– это полный токъ въ нагрузкѣ:
Измѣнимъ выраженія [3] и [4] такъ, чтобъ число подмѣнъ при послѣдующемъ счетѣ стало наименьшимъ:
Похожие вопросы
Предмет: Математика,
автор: Gamma101
Предмет: Математика,
автор: tokkugawa
Предмет: Английский язык,
автор: likasotnikova08
Предмет: Биология,
автор: ZvezdaSunny
Предмет: Математика,
автор: halakaeva0913