Предмет: Алгебра,
автор: Snegir1111
Срочно!!! Помогите решить пожалуйста.
1) 9^x-23*3^((x-3)/2)=4*3^(-x)
2) 25^sin^2x+100=5*(1/5)^cos^2x-2
Приложения:
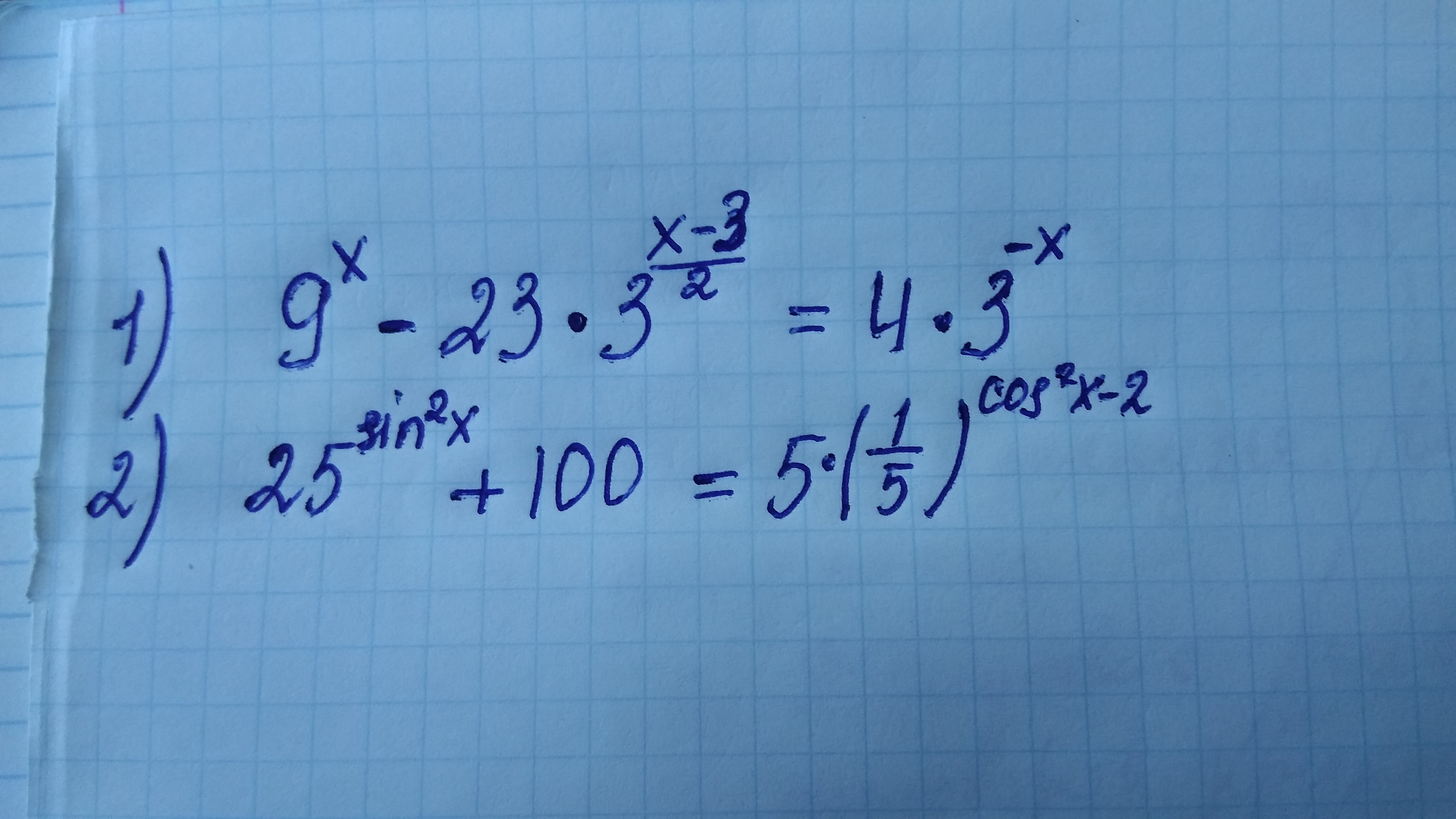
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: gasselena94
Предмет: Геометрия,
автор: rty777
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: mixa100
Предмет: Химия,
автор: Linazz