Предмет: Алгебра,
автор: artem7770
решите
пж срочно надо
желательно во вложении
Приложения:
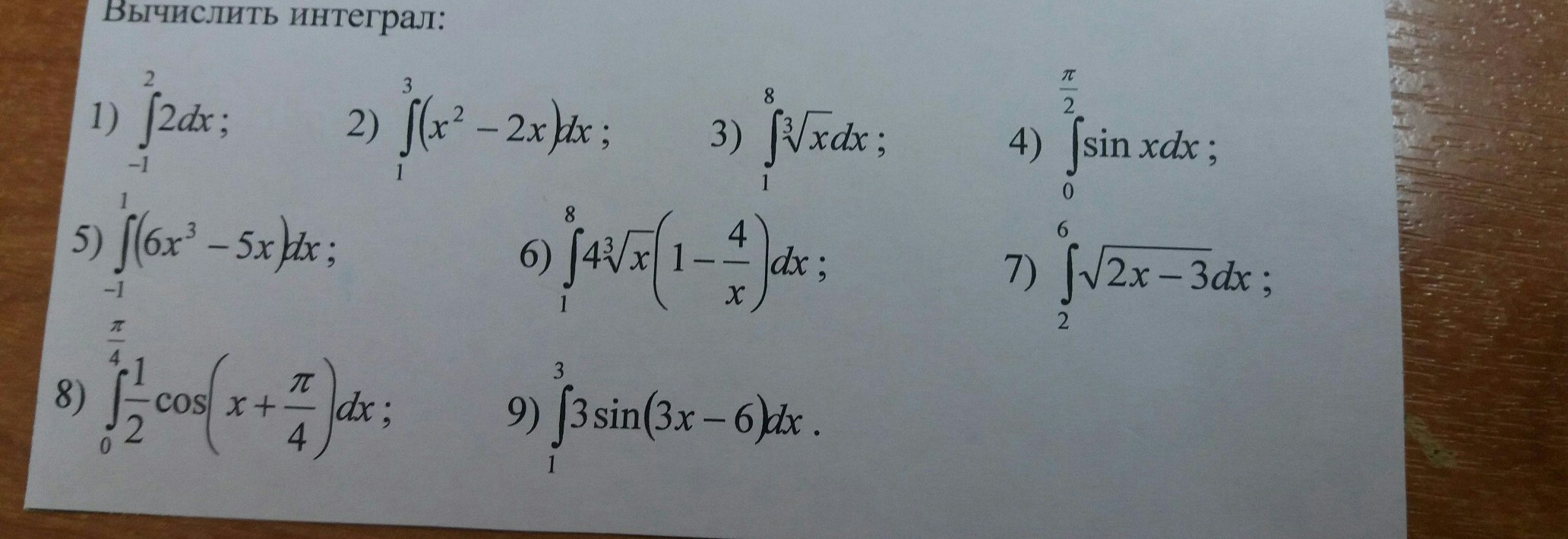
Ответы
Автор ответа:
0
Автор ответа:
0
ничего не понятно
Автор ответа:
0
Перезагрузи страницу и увидишь матем. текст.
Похожие вопросы
Предмет: Русский язык,
автор: aroslavtuzlukov9097
Предмет: Математика,
автор: irinoshka2007ksenia1
Предмет: Алгебра,
автор: vitaaa174
Предмет: Алгебра,
автор: babaeva18032001