Question

доказательства площади треугольника

Answer 1

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне S = a • h.
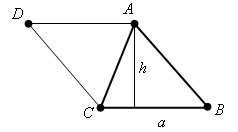
Пусть ABC – данный треугольник. Дополним его до параллелограмма ABCD. 
Площадь параллелограмма равна сумме площадей треугольников ABC и CDA. Так как эти треугольники равны, то площадь параллелограмма равна удвоенной площади треугольника ABC. Высота параллелограмма, соответствующая стороне CB, равна высоте треугольника, проведенной к стороне CB. Отсюда следует утверждение теоремы, и S=1/2a*h