Предмет: Алгебра,
автор: AnaBek
решите неравенство
x^4-6x^3+11x^2-6x< 0
Ответы
Автор ответа:
0
x⁴-6x³+11x²-6x<0
x(x³-6x²+11x-6)<0
Видим, что в x³-6x²+11x-6=0 корнем уравнения является 1. Разделим данный многочлен на (x-1)
(см. вложение)
x(x-1)(x²-5x+6)<0
Рассмотрим x²-5x+6=0
D=5²-4*6=1
x=(5+1)/2=3
x=(5-1)/2=2
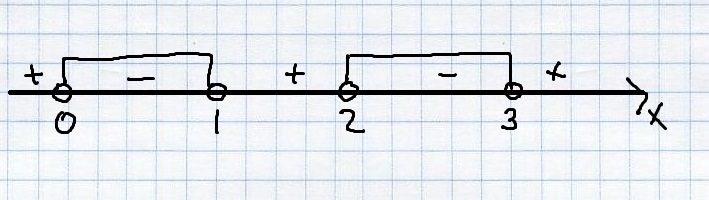
x(x-1)(x-2)(x-3)<0
(см. вложение)
x∈(0;1)U(2;3)
x(x³-6x²+11x-6)<0
Видим, что в x³-6x²+11x-6=0 корнем уравнения является 1. Разделим данный многочлен на (x-1)
(см. вложение)
x(x-1)(x²-5x+6)<0
Рассмотрим x²-5x+6=0
D=5²-4*6=1
x=(5+1)/2=3
x=(5-1)/2=2
x(x-1)(x-2)(x-3)<0
(см. вложение)
x∈(0;1)U(2;3)
Приложения:
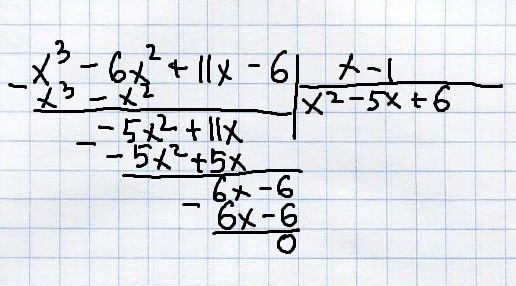
Похожие вопросы
Предмет: Русский язык,
автор: faridaejbova27
Предмет: Математика,
автор: soveaq
Предмет: Биология,
автор: Аноним
Предмет: Физика,
автор: Аноним