Question

Даю 100 балов кто ответит и нарисует какой график получится
Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её.
16х²-9у²-64х-54у-161=0

Answer 1

16х²-9у²-64х-54у-161=0
Выделяем полные квадраты
(16х²-16*2*2x+16*2²)-(9у²+9*2*3y+9*3²)-144=0
16(х²-2*2x+2²)-9(у²+2*3y+3²)=144
16(х-2)²-9(у+3)=144
теперь приведем к каноническому виду - разделим на 144
$frac{(x-2)^2}{3^2} - frac{(y+3)^2}{4^2}=1$
это гипербола с центром в точке (2;-3) и асимптотами $y= frac{4}{3}(x-2)-3$  и  $y= - frac{4}{3}(x-2)-3$ 

Answer 2

(16x²-64x+64)-64-(9y²+54y+81)+81-161=0
16(x²-4x+4)-9(y²+6y+9)=144
16(x-2)²-9(y+3)²=144/144
(x-2)²/9-(y+3)²/16=1
(х-2)²/3²-(у+3)²/4²
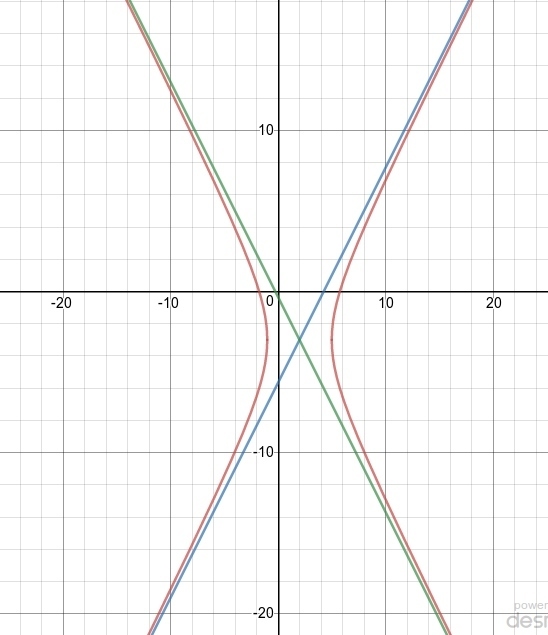
Получили уравнение гиперболы с центром (2;-3)
Асимптоты :y=-4/3*(x-2)-3;y=4/3*(x-2)-3

1dbd93e47061430a11fb7a681952889f.docx