Предмет: Алгебра,
автор: lanila
помогиите, пожалуйста)
Приложения:
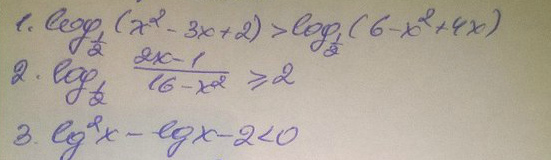
Ответы
Автор ответа:
0
1.

ОДЗ:
+ - +
{x²-3x+2>0 {(x-2)(x-1)>0 ------(1)----------(2)----------->
//////// /////////////
- + -
{6-x²+4x>0 {(x-2+√10)(x-2-√10)>0 ------(2-√10)------------(2+√10)------->
////////////////////////
Общее:
x∈(2-√10; 1)∪(2; 2+√10)



+ - +
-------(-0.5)-----------------(4)-------------->
///////////////////////////
Ответ: (-0,5; 1)∪(2; 4)
2.

ОДЗ:

+ - + -
--------(-4)----------(¹/₂)----------(4)--------->
//////////// /////////////////
x∈(-∞; -4)∪(¹/₂; 4)

- + - + -
----------[-10]----------(-4)-----------[2]-----------(4)-------->
//////////////// /////////////////// //////////
Ответ: (-∞; -10]∪(¹/₂; 2]
3.

ОДЗ: х>0
Замена:

+ - +
----------(-1)--------------(2)----------->
/////////////////////

\\\\\\\XXXXXXXXX///////////////
---------(0.1)-------------(100)----------->
Ответ: (0,1; 100)
ОДЗ:
+ - +
{x²-3x+2>0 {(x-2)(x-1)>0 ------(1)----------(2)----------->
//////// /////////////
- + -
{6-x²+4x>0 {(x-2+√10)(x-2-√10)>0 ------(2-√10)------------(2+√10)------->
////////////////////////
Общее:
x∈(2-√10; 1)∪(2; 2+√10)
+ - +
-------(-0.5)-----------------(4)-------------->
///////////////////////////
Ответ: (-0,5; 1)∪(2; 4)
2.
ОДЗ:
+ - + -
--------(-4)----------(¹/₂)----------(4)--------->
//////////// /////////////////
x∈(-∞; -4)∪(¹/₂; 4)
- + - + -
----------[-10]----------(-4)-----------[2]-----------(4)-------->
//////////////// /////////////////// //////////
Ответ: (-∞; -10]∪(¹/₂; 2]
3.
ОДЗ: х>0
Замена:
+ - +
----------(-1)--------------(2)----------->
/////////////////////
\\\\\\\XXXXXXXXX///////////////
---------(0.1)-------------(100)----------->
Ответ: (0,1; 100)
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: История,
автор: pashalolpop02
Предмет: Информатика,
автор: LoverHeadshots
Предмет: Литература,
автор: ЛераМорозова1368