Предмет: Геометрия,
автор: xolost
В треугольнике АВС проведена биссектриса AL, угол ALC равен 75 градусов, угол АВС равен 35 градусов. Найдите угол АCВ. Ответ дайте в градусах.
Ответы
Автор ответа:
0
∠ALB = 180° - ∠ALC = 180° - 75° = 105° - по свойству смежных углов.
∠LAB = 180° - ∠ALB - ∠ABC = 180° - 105° - 35° = 40°.
∠BAL = ∠CAL = 1/2∠BAC, т.к. AL - биссектриса. Тогда ∠BAC = 2∠BAL = 2•40° = 80°
∠ACB = 180° - ∠ABC - ∠BAC = 180° - 80° - 35° = 65°.
Ответ: 65°.
∠LAB = 180° - ∠ALB - ∠ABC = 180° - 105° - 35° = 40°.
∠BAL = ∠CAL = 1/2∠BAC, т.к. AL - биссектриса. Тогда ∠BAC = 2∠BAL = 2•40° = 80°
∠ACB = 180° - ∠ABC - ∠BAC = 180° - 80° - 35° = 65°.
Ответ: 65°.
Автор ответа:
0
Решение:
Угол ALC + угол ABL= 180°. Угол ABL= 180° - 75° = 105°. Рассмотрим треугольник ABL: угол ABL =35°, угол ALB = 105°. Тогда угол BAL = 180° - (105°+35°) = 40°. Поскольку AL - бисектриса, то угол BAL = углу LAC = 40°. Рассмотрим треугольник ACL: угол ALC = 75°, угол LAC = 40°, тогда угол ACL = 180° - (75°+40°)= 65°.
Ответ: 65°.
Угол ALC + угол ABL= 180°. Угол ABL= 180° - 75° = 105°. Рассмотрим треугольник ABL: угол ABL =35°, угол ALB = 105°. Тогда угол BAL = 180° - (105°+35°) = 40°. Поскольку AL - бисектриса, то угол BAL = углу LAC = 40°. Рассмотрим треугольник ACL: угол ALC = 75°, угол LAC = 40°, тогда угол ACL = 180° - (75°+40°)= 65°.
Ответ: 65°.
Приложения:
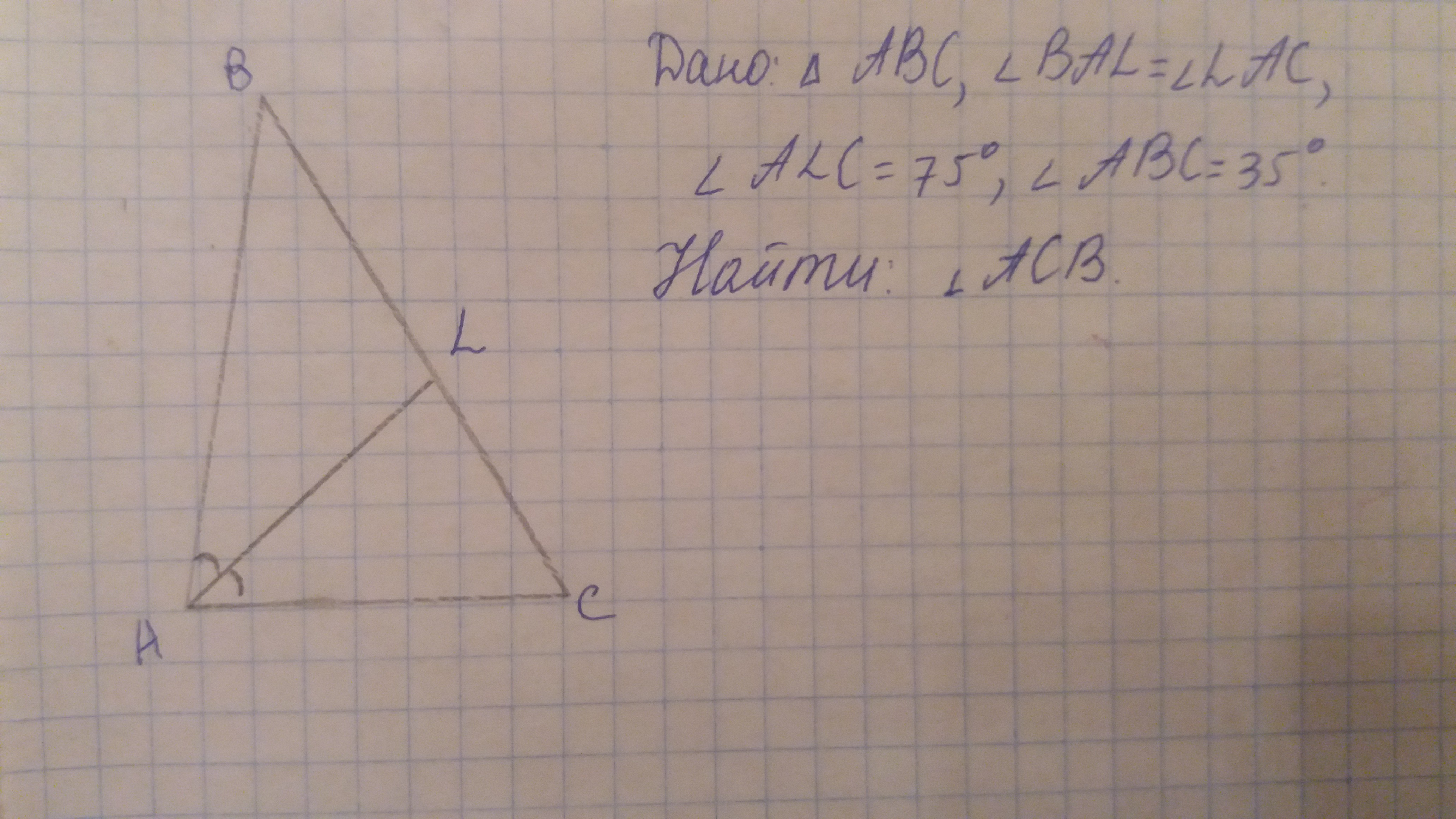
Похожие вопросы
Предмет: Английский язык,
автор: VladimirPPutin
Предмет: Математика,
автор: polina7888889
Предмет: Литература,
автор: aya11asem
Предмет: Химия,
автор: valiaco2015
Предмет: Математика,
автор: tchistyackova1