Question

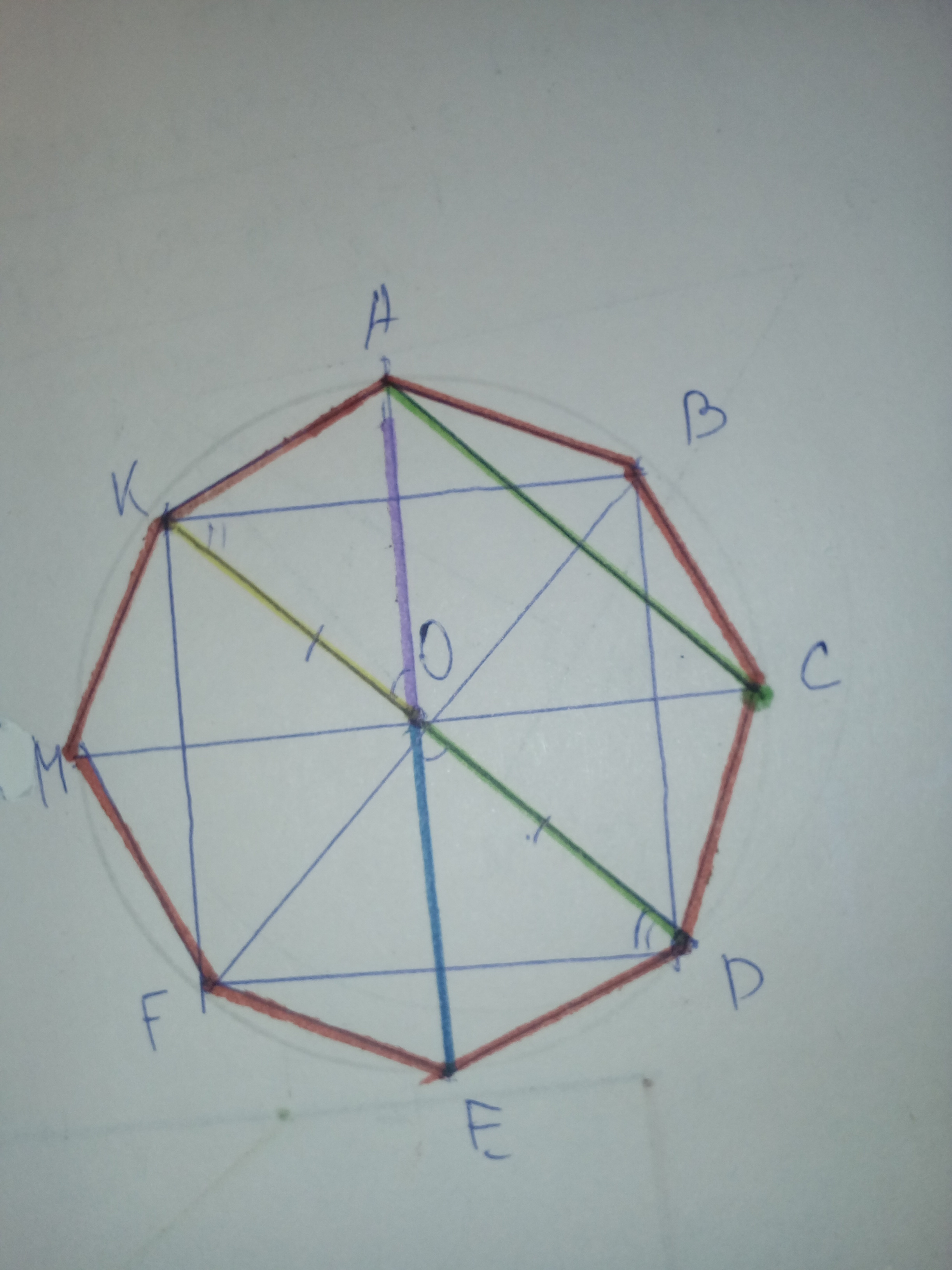
дан правильный восьмиугольник ABCDEFMK
1) докажите что диагональ AE является диаметром описанной окружности восьмиугольника
2) найдите диагональ AC если радиус описанной окружности равен 3 корень из 2 см

Answer 1

KBDE - вписанный квадрат => FD пересекается с KO в точке О, где О будет являться центром описанной окружности.
∆KOA = AOB = ∆BOC = ... = EOD (т.к. стороны у них равны, а О - центр вписанной окружности, который является точкой пересечения биссектрис углов).
Значит, АО = ОЕ = R => AO + OE = AE = 2R = D.

2) Диагональ АС будет являться гипотенузой в прямоугольном равнобедренном треугольнике AOC. По теореме Пифагора:
AC = √(3√2)² + (3√2)² = √18 + 18 = √36 = 6см.
Ответ: 6 см.