Предмет: Математика,
автор: 5Апельсинчик5
Помогите пожалуйста решить
Приложения:
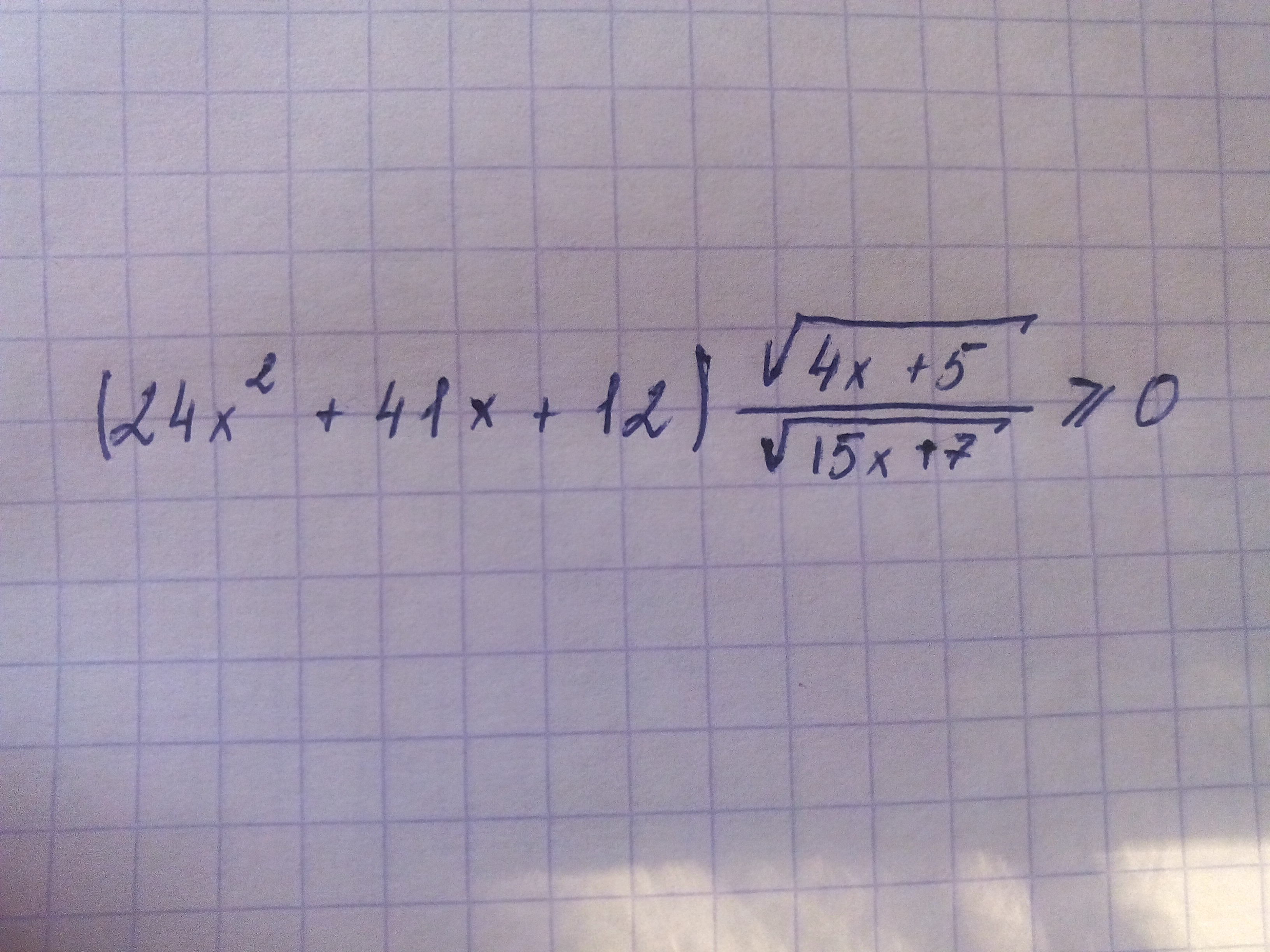
Ответы
Автор ответа:
0
ОДЗ:
4x+5≥0
4x≥-5
x≥-1.25
15x+7>0
15x>-7
x>
общее: x>
Найдем нули функции:
Решим неравенство методом интервалов и найдём решение, общее с ОДЗ:
- - - - +
////////////////////////////////////////////////////////
---------[-4/3]---------[-1.25]-----------(-7/15)----------[-3/8]---------->
\\\\\\\\\\\\\\\\
x∈[-
Похожие вопросы
Предмет: Математика,
автор: dianasysydoruk
Предмет: Математика,
автор: surmagull
Предмет: Русский язык,
автор: Аноним
Предмет: Обществознание,
автор: artemsevalskov
Предмет: История,
автор: AlinaWhite