Предмет: Геометрия,
автор: Ксения282325
В параллелограмме одна из сторон равна 10 см, а один из углов 30 градусов. Найдите площадь параллелограмма, если его периметр равен 56
Ответы
Автор ответа:
0
Площадь параллелограмма равна произведению высоты на сторону
Для начала найдём другую сторону: в параллелограмме противоположные стороны равны, значит, периметр P=a+b+c+d=2a+2b=2(a+b)
Мы знаем P=56 и a=10
Значит, 56=2(10+b)
56/2=10+b
28=10+b
b=28-10=18
Вторая сторона равна 18 см
Теперь найдём высоту:
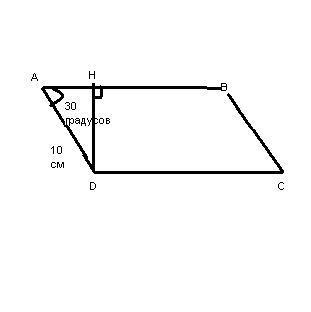
Рассмотрим ΔADH (рисунок ниже):
Если это прямоугольный треугольник, и в нём угол 30°, то противоположный катет равен половине гипотенузы, т.е. HD=AD/2
AD = 10 см
Значит, HD=5 см, то есть высота равна 5 см
Теперь можно найти площадь: 18*5=60 см
Ответ: 60 квадратных сантиметров
Для начала найдём другую сторону: в параллелограмме противоположные стороны равны, значит, периметр P=a+b+c+d=2a+2b=2(a+b)
Мы знаем P=56 и a=10
Значит, 56=2(10+b)
56/2=10+b
28=10+b
b=28-10=18
Вторая сторона равна 18 см
Теперь найдём высоту:
Рассмотрим ΔADH (рисунок ниже):
Если это прямоугольный треугольник, и в нём угол 30°, то противоположный катет равен половине гипотенузы, т.е. HD=AD/2
AD = 10 см
Значит, HD=5 см, то есть высота равна 5 см
Теперь можно найти площадь: 18*5=60 см
Ответ: 60 квадратных сантиметров
Приложения:
Похожие вопросы
Предмет: Биология,
автор: Qwerty333333
Предмет: География,
автор: arz02072006
Предмет: Английский язык,
автор: Abobus229
Предмет: Математика,
автор: anastasiyaton