Предмет: Алгебра,
автор: Vikyyy
Две фабрики выпускают одинаковые стёкла для автомобильных фар.Первая фабрика выпускает 60 % этих стёкол,вторая 40 %.Среди стёкол,выпускаемых первой фабрикой,брак состовляет 3%.Cреди стёкол,выпускаемых второй фабрикой,брак состовляет 1%.Найдите вероятность того,что случайно купленное в магазине стекло окажется бракованным.
Ответы
Автор ответа:
0
Выполнив несколько не сложных вычислений и применив формулу ПОЛНОЙ ВЕРОЯТНОСТИ и формулу БАЙЕСА мы сможем ответить на гораздо больше вопросов, чем задано в условии задачи.
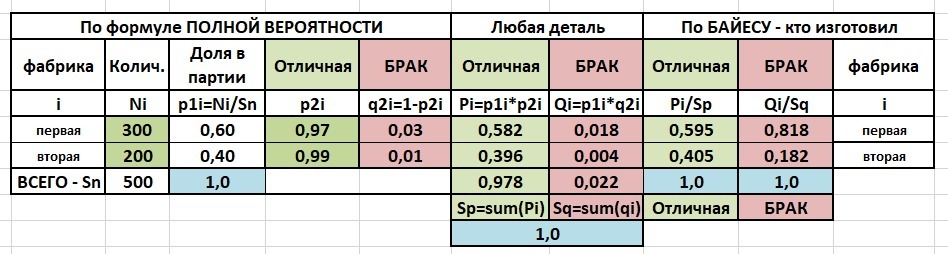
ТАБЛИЦА для расчета приведена в приложении
РЕШЕНИЕ
Задача состоит из двух событий -
1) выбрать СЛУЧАЙНУЮ - р(1,i) - задана процентами в производстве фабрик.
Её можно рассчитать по количеству продукции (200/500 = 0,4 = 40%- дано)
p1,1 = 0.6 p1,2=0.4
Проверяем на полную вероятность - сумма равна = 0,4 + 0,6 = 1 - правильно - других поставщиков нет
2) случайную и БРАКОВАННУЮ.
Вероятность брака - q2i - дана
q2,1 = 0.03, q2,2 = 0.1 - вероятность брака - дана.
Вероятность годных деталей вычисляем по формуле
р2,1 = 1 - q2,1 = 0.97, p2,2 = 0.99
Вероятность двух независимых событий равна произведению каждого из них или по формуле
Для брака - Q1 = 0,6*0.03 = 0.018 Q2 = 0.4*0.01 = 0.004
и сумма -
Sq = 0,018+0,004 = 0,022 = 2,2% - вероятность случайной и бракованной детали - ОТВЕТ
Продолжим расчет
Для годных деталей получаем: Sp =0,582+0,396 = 0.978 = 97.8%
.Проверяем на полную вероятность - сумма равна 1 - правильно.
А теперь можно и найти кто выпустил этот брак по формуле Байеса.
Всего брака - 0,022 из них первая фабрика - 0,018 или
0,018 : 0,022 = 0,818 = 81,8% - брак от первой фабрики.
А годные детали выпускает вторая - 0,396/0,978 = 0,405 = 40,5%
ТАБЛИЦА для расчета приведена в приложении
РЕШЕНИЕ
Задача состоит из двух событий -
1) выбрать СЛУЧАЙНУЮ - р(1,i) - задана процентами в производстве фабрик.
Её можно рассчитать по количеству продукции (200/500 = 0,4 = 40%- дано)
p1,1 = 0.6 p1,2=0.4
Проверяем на полную вероятность - сумма равна = 0,4 + 0,6 = 1 - правильно - других поставщиков нет
2) случайную и БРАКОВАННУЮ.
Вероятность брака - q2i - дана
q2,1 = 0.03, q2,2 = 0.1 - вероятность брака - дана.
Вероятность годных деталей вычисляем по формуле
р2,1 = 1 - q2,1 = 0.97, p2,2 = 0.99
Вероятность двух независимых событий равна произведению каждого из них или по формуле
Для брака - Q1 = 0,6*0.03 = 0.018 Q2 = 0.4*0.01 = 0.004
и сумма -
Sq = 0,018+0,004 = 0,022 = 2,2% - вероятность случайной и бракованной детали - ОТВЕТ
Продолжим расчет
Для годных деталей получаем: Sp =0,582+0,396 = 0.978 = 97.8%
.Проверяем на полную вероятность - сумма равна 1 - правильно.
А теперь можно и найти кто выпустил этот брак по формуле Байеса.
Всего брака - 0,022 из них первая фабрика - 0,018 или
0,018 : 0,022 = 0,818 = 81,8% - брак от первой фабрики.
А годные детали выпускает вторая - 0,396/0,978 = 0,405 = 40,5%
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: bngghj
Предмет: История,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: мар31
Предмет: Алгебра,
автор: Cymrak