Предмет: Другие предметы,
автор: kristina1998014
Помогите пожалуйста. Докажите методом математической индукции что для любого положительно числа N справедлива формула
Приложения:
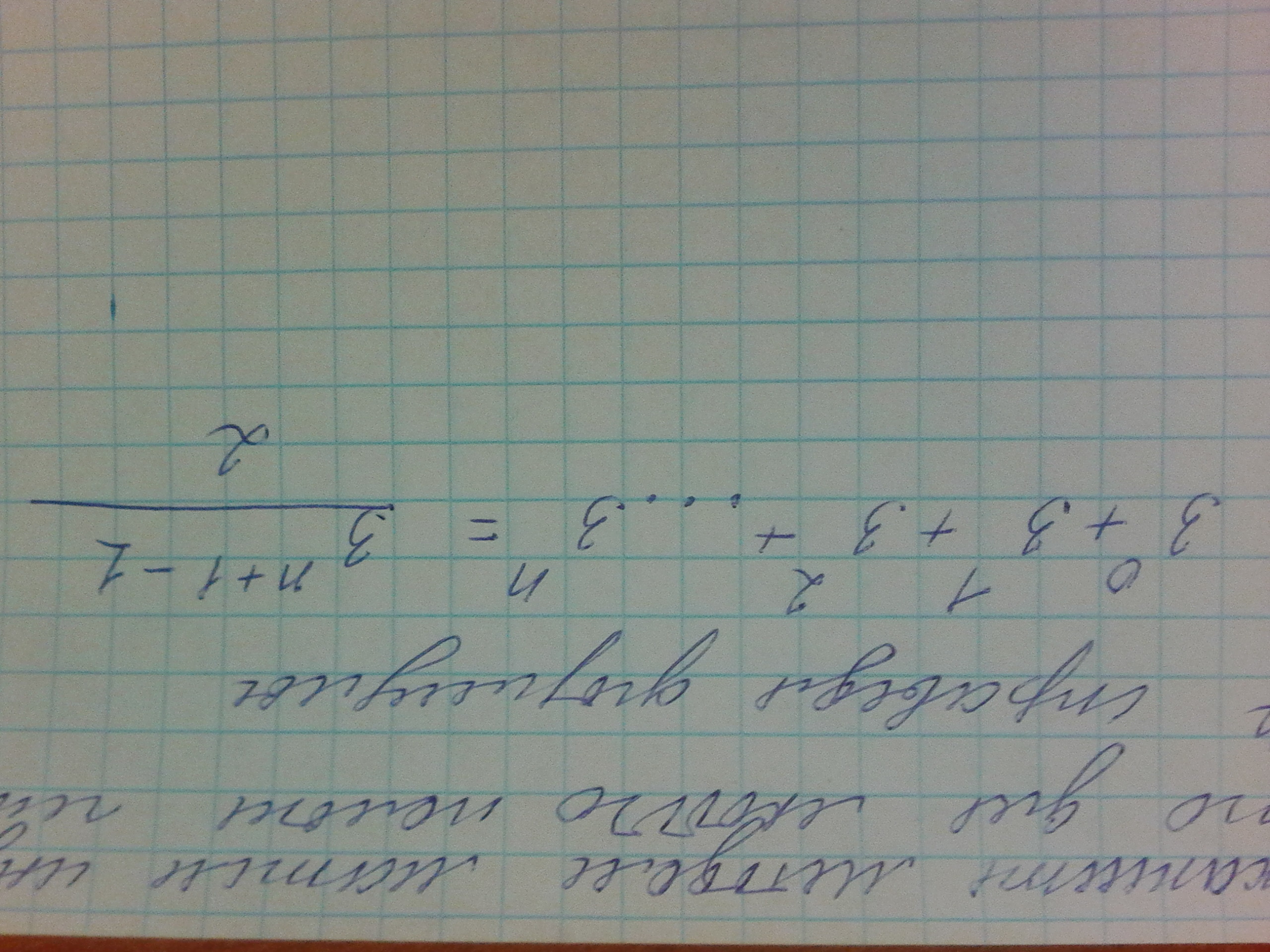
Ответы
Автор ответа:
1
1. Проверим формулу для n=1
 .Равенство верное.
.Равенство верное.
2. Допустим, что формула верна для любого неотрицательного n.
верна для любого неотрицательного n.
3. Проверяем, верна ли формула для n+1. Чтобы получить сумму для n+1 членов последовательности, надо к сумме n членов прибавить
 .
.
Всё!
С наступающим Новым годом!
2. Допустим, что формула
3. Проверяем, верна ли формула для n+1. Чтобы получить сумму для n+1 членов последовательности, надо к сумме n членов прибавить
Всё!
С наступающим Новым годом!
kristina1998014:
Спасибо большое) и вас с наступающим Новым годом!!!)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: karolinakotova1025
Предмет: Українська мова,
автор: DrakoshaVel
Предмет: Қазақ тiлi,
автор: ssuzuki541
Предмет: Математика,
автор: Levka444