Предмет: Математика,
автор: LJJIK
Какова наименьшая возможная длина апофемы правильной треугольной пирамиды,имеющий объем 1 см^3 ?
Ответы
Автор ответа:
0
Если треугольная пирамида правильная, то в основании лежит правильный треугольник.
Площадь правильного треугольника:

где а - сторона треугольника.
Объем равен:

Отсюда выражаем высоту h:

подставляем формулу площади треугольника и V=1 см³

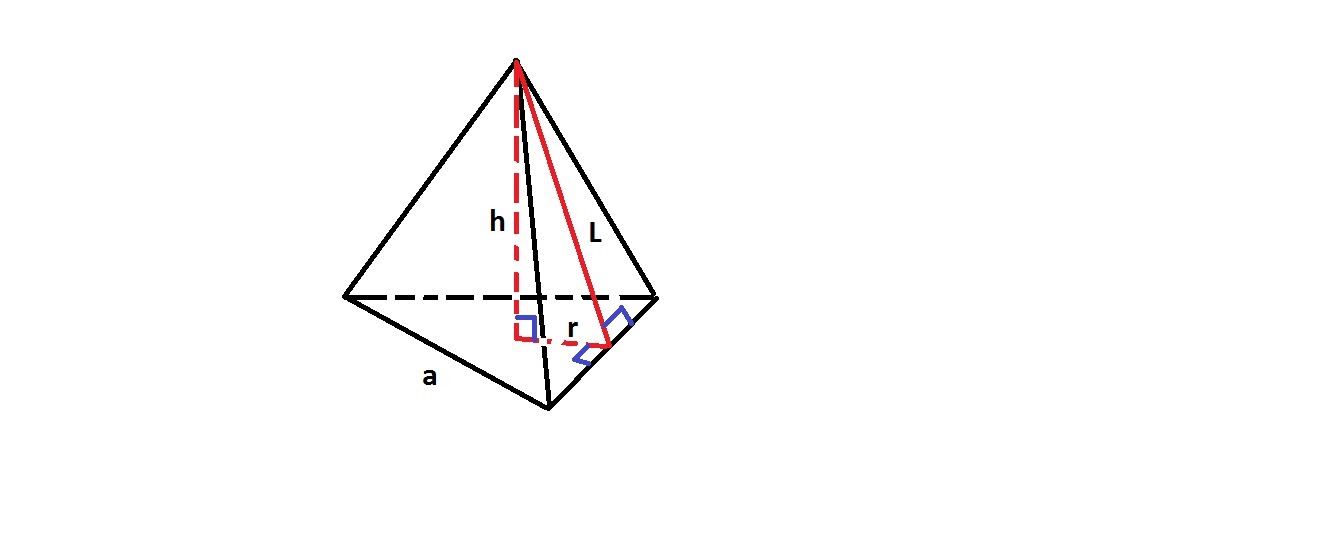
Апофему L можно найти по теореме Пифагора в прямоугольном треугольнике, где катетами являются высота пирамиды h и радиус вписанной окружности r

Радиус вписанной окружности в правильный треугольник:

В итоге получилась функция вида:

Чтобы найти наименьшее значение апофемы, то есть наименьшее значение функции L(a), нужно найти точку минимума. Для этого надо взять производную:

Находим ОДЗ производной:
Подкоренное выражение должно быть больше либо равен нулю, но так как корень квадратный стоит в знаменателе, значит Подкоренное выражение должно быть строго больше нуля.
Так как a⁶≥0 и а⁴≥0, значит
 - при любых а, кроме а=0
- при любых а, кроме а=0
Знаменатель не должен равняться нулю, значит

теперь приравниваем производную к нулю

Было сказано, что

значит

это выражение не имеет корней, поэтому все уравнение можно на него разделить:
![frac{a^6-1152}{6a^5} =0 \ \ a^6-1152=0 \ \ a^6=1152 \ \ a= ^+_-sqrt[6]{1152} \ \ frac{a^6-1152}{6a^5} =0 \ \ a^6-1152=0 \ \ a^6=1152 \ \ a= ^+_-sqrt[6]{1152} \ \](https://tex.z-dn.net/?f=frac%7Ba%5E6-1152%7D%7B6a%5E5%7D+%3D0+%5C++%5C+a%5E6-1152%3D0+%5C++%5C+a%5E6%3D1152+%5C++%5C+a%3D+%5E%2B_-sqrt%5B6%5D%7B1152%7D++%5C++%5C+)
Откладываем все корни уравнения и точки из ОДЗ на координатной оси и методом интервалов определяем точки минимума
![---[ - sqrt[6]{1152} ]+++(0)---[ sqrt[6]{1152} ]+++ textgreater a ---[ - sqrt[6]{1152} ]+++(0)---[ sqrt[6]{1152} ]+++ textgreater a](https://tex.z-dn.net/?f=---%5B+-+sqrt%5B6%5D%7B1152%7D+%5D%2B%2B%2B%280%29---%5B++sqrt%5B6%5D%7B1152%7D+%5D%2B%2B%2B+textgreater++a)
получились две точки минимума:
![a=sqrt[6]{1152} \ a=- sqrt[6]{1152} a=sqrt[6]{1152} \ a=- sqrt[6]{1152}](https://tex.z-dn.net/?f=a%3Dsqrt%5B6%5D%7B1152%7D+%5C+a%3D-++sqrt%5B6%5D%7B1152%7D+)
Вторая точка точка нам не подходит, так как сторона не может быть отрицательной.
Наконец находим минимальное значении функции, и тем самым наименьшую длину апофемы
![L(sqrt[6]{1152} )= sqrt{ frac{(sqrt[6]{1152} )^6+576}{12*(sqrt[6]{1152} )^4} }= sqrt{ frac{1152+576}{12*1152^{ frac{4}{6} } } }= sqrt{ frac{1728}{12*1152^{ frac{2}{3}} }} = \ \ = sqrt{ frac{144}{1152^{ frac{2}{3}} } }= frac{ sqrt{144} }{ sqrt{1152^{ frac{2}{3} }} }= frac{12}{1152^{ frac{1}{3} }} = frac{12}{ sqrt[3]{1152} } \ \ OTBET: frac{12}{ sqrt[3]{1152} } L(sqrt[6]{1152} )= sqrt{ frac{(sqrt[6]{1152} )^6+576}{12*(sqrt[6]{1152} )^4} }= sqrt{ frac{1152+576}{12*1152^{ frac{4}{6} } } }= sqrt{ frac{1728}{12*1152^{ frac{2}{3}} }} = \ \ = sqrt{ frac{144}{1152^{ frac{2}{3}} } }= frac{ sqrt{144} }{ sqrt{1152^{ frac{2}{3} }} }= frac{12}{1152^{ frac{1}{3} }} = frac{12}{ sqrt[3]{1152} } \ \ OTBET: frac{12}{ sqrt[3]{1152} }](https://tex.z-dn.net/?f=L%28sqrt%5B6%5D%7B1152%7D+%29%3D++sqrt%7B+frac%7B%28sqrt%5B6%5D%7B1152%7D+%29%5E6%2B576%7D%7B12%2A%28sqrt%5B6%5D%7B1152%7D+%29%5E4%7D+%7D%3D+sqrt%7B+frac%7B1152%2B576%7D%7B12%2A1152%5E%7B+frac%7B4%7D%7B6%7D+%7D+%7D+%7D%3D+sqrt%7B+frac%7B1728%7D%7B12%2A1152%5E%7B+frac%7B2%7D%7B3%7D%7D+%7D%7D+%3D+%5C++%5C+%3D+sqrt%7B+frac%7B144%7D%7B1152%5E%7B+frac%7B2%7D%7B3%7D%7D+%7D+%7D%3D+frac%7B+sqrt%7B144%7D+%7D%7B+sqrt%7B1152%5E%7B+frac%7B2%7D%7B3%7D+%7D%7D+%7D%3D+frac%7B12%7D%7B1152%5E%7B+frac%7B1%7D%7B3%7D+%7D%7D++%3D+frac%7B12%7D%7B+sqrt%5B3%5D%7B1152%7D+%7D++%5C++%5C+OTBET%3A++frac%7B12%7D%7B+sqrt%5B3%5D%7B1152%7D+%7D++)
Площадь правильного треугольника:
где а - сторона треугольника.
Объем равен:
Отсюда выражаем высоту h:
подставляем формулу площади треугольника и V=1 см³
Апофему L можно найти по теореме Пифагора в прямоугольном треугольнике, где катетами являются высота пирамиды h и радиус вписанной окружности r
Радиус вписанной окружности в правильный треугольник:
В итоге получилась функция вида:
Чтобы найти наименьшее значение апофемы, то есть наименьшее значение функции L(a), нужно найти точку минимума. Для этого надо взять производную:
Находим ОДЗ производной:
Подкоренное выражение должно быть больше либо равен нулю, но так как корень квадратный стоит в знаменателе, значит Подкоренное выражение должно быть строго больше нуля.
Так как a⁶≥0 и а⁴≥0, значит
Знаменатель не должен равняться нулю, значит
теперь приравниваем производную к нулю
Было сказано, что
значит
это выражение не имеет корней, поэтому все уравнение можно на него разделить:
Откладываем все корни уравнения и точки из ОДЗ на координатной оси и методом интервалов определяем точки минимума
получились две точки минимума:
Вторая точка точка нам не подходит, так как сторона не может быть отрицательной.
Наконец находим минимальное значении функции, и тем самым наименьшую длину апофемы
Приложения:
Похожие вопросы
Предмет: Математика,
автор: lvi314080
Предмет: История,
автор: dzurykveronika2605
Предмет: Русский язык,
автор: cmotpim
Предмет: География,
автор: Tana251
Предмет: Математика,
автор: aneka0097