4. Взаимное расположение двух прямых в пространстве.
5. Признак скрещивающихся прямых (формулировка, доказательство).
6. Определение параллельности прямой и плоскости (взаимное расположение прямой и плоскости).
Ответы
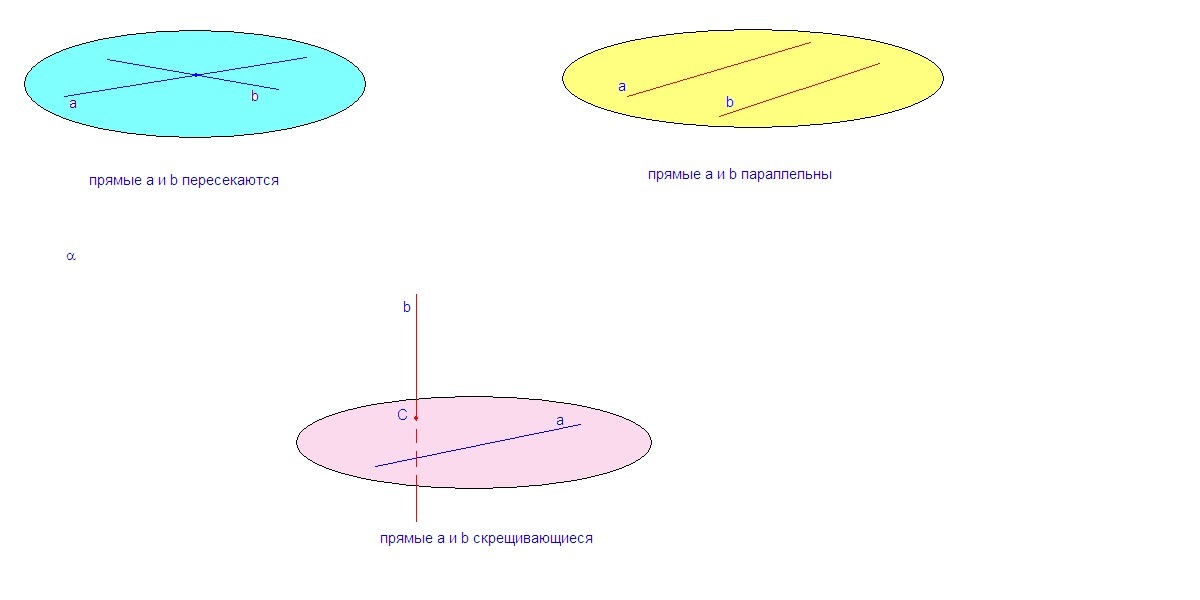
4. Существуют три возможных варианта расположения прямых в пространстве:
- прямые пересекаются, т.е. имеют одну общую точку;
- прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;
- прямые скрещивающиеся, т.е. прямые не пересекаются, но через них нельзя провести плоскость.
5. Признак скрещивающихся прямых:
Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то прямые скрещивающиеся.
Дано: а⊂α, b∩α = C, C∉a.
Доказать: прямые а и b скрещивающиеся.
Доказательство:
Надо доказать, что не существует плоскости, в которой лежат обе прямые.
Доказательство от противного: предположим, что существует некоторая плоскость β, в которой лежат обе прямые. Тогда в этой плоскости будут лежать прямая а и точка С. Но через прямую и точку, не лежащую на ней, проходит единственная плоскость - α. Значит плоскости β не существует. Т.е. прямые а и b скрещивающиеся.
6. Прямая называется параллельной плоскости, если она не имеет общих точек с плоскостью.