Предмет: Алгебра,
автор: Zontuk1999
Найти наибольшее значение функции на интервалах.
Приложения:
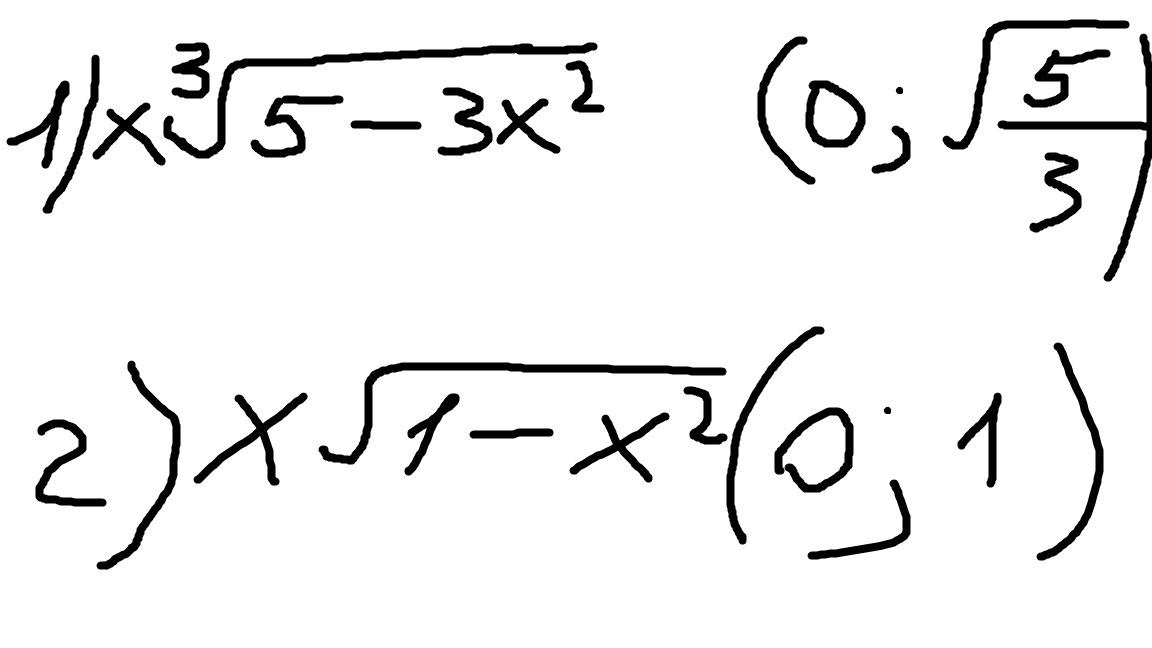
Ответы
Автор ответа:
0
1
(∛(5x³-3x^5))`=(15x²-15x^4)/3(5x³-3x^5)²=0
15x²(1-x)(1+x)=0
x=0 x=1 x=-1
_ + + _
---------------(1)--------------(0)----------------(1)----------------
\\\\\\\\\\\\\\\\\\\\\\\
возр убыв
наиб при х=1 равняется ∛2
2
(√(x²-x^4))`=(2x-4x³)/2√(x²-x^4)=0
2x(1-√2x)(1+√2x)=0
x=0 x=1/√2 x=-1/√2
+ _ + _
---------------(-1/√2)-----------(0)----------------(1/√2)----------------
\\\\\\\\\\\\\\\\\\\\\\\
возр убыв
наиб при х=1/√2 равняется 1/2
(∛(5x³-3x^5))`=(15x²-15x^4)/3(5x³-3x^5)²=0
15x²(1-x)(1+x)=0
x=0 x=1 x=-1
_ + + _
---------------(1)--------------(0)----------------(1)----------------
\\\\\\\\\\\\\\\\\\\\\\\
возр убыв
наиб при х=1 равняется ∛2
2
(√(x²-x^4))`=(2x-4x³)/2√(x²-x^4)=0
2x(1-√2x)(1+√2x)=0
x=0 x=1/√2 x=-1/√2
+ _ + _
---------------(-1/√2)-----------(0)----------------(1/√2)----------------
\\\\\\\\\\\\\\\\\\\\\\\
возр убыв
наиб при х=1/√2 равняется 1/2
Похожие вопросы