Предмет: Алгебра,
автор: CatLove2014
Решите систему уравнений.
Приложения:
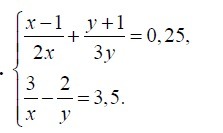
Ответы
Автор ответа:
0
Сразу отметим, что х≠0 и у≠0.
Получили, что первое уравнение представляет из себя второе, домноженное на (-1). Значит системе удовлетворяют все числа х и у при условии x≠0 и у≠0.
Автор ответа:
0
Спасибо!
Похожие вопросы
Предмет: История,
автор: jeufkni8rg
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: karsybaevarabiga549
Предмет: Математика,
автор: fffcvhurdf
Предмет: Обществознание,
автор: natalistoyad