По горизонтальной трубе переменного сечения течет жидкость плотностью p. Определите разность давлений "дельта"p в двух сечениях трубы площадями S1 и S2 (S1>S2) если объем жидкости протекающей через поперечное сечение трубы в еденицу времени Q.
Ответы
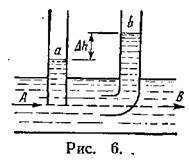
а) Способ измерения скорости
движения жидкости.
Представим, что в движущуюся жидкость опущены две трубки малого сечения, причем, плоскость поперечного сечения одной из них параллельна направлению скорости движения жидкости v, а другая (трубка Пито) изогнута так, что плоскость сечения изогнутой части
перпендикулярна направлению скорости течения (рис.6). Подъем жидкости в прямой трубке на высоту h1обусловлен лишь статическим давлением Рc, которое можно определить по формуле:
Pc= ρgh1.
В трубке Пито подъем жидкости на высоту h2обусловлен полным давлением Рп- в данном случае суммой статического Рси динамического Рддавлений (течение происходит горизонтально и весовое давление не учитывается). Следовательно:
Рп= Рс+ Рд;
ρgh2 = ρgh1 + ρv2/2
Из последней формулы находим линейную скорость жидкости:
.
Таким образом, по измеренной разности уровней жидкости в прямой и
изогнутой трубках определяется скорость течения жидкости. Этим же
методом определяют и скорость самолета относительно воздуха, катера относительно воды и др.
Ответ: v=1,4 МС