Предмет: Алгебра,
автор: Vayar
Логарифмическое уравнение.
Распишите решение.
Фото внизу.
Приложения:
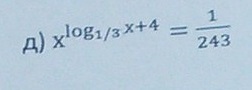
Ответы
Автор ответа:
0
заметим что одз па апределению логарифма x>0
x^((log1/3 x)+4)=1/243
x^(log1/3 x)*x^4)=1/3^5 лево право больше 0 пролагарифмируем обе части
основание пусть 1/3 будет
log1/3 ( x^(log1/3 x)*x^4)) = log1/3 (1/3^5)
log1/3 ( x^(log1/3 x)) + log 1/3 x^4 = 5
log1/3 x * log1/3 x + 4* log 1/3 x -5=0
log 1/3 x = t
t^2+4t - 5 =0
D=16+20=36
t12= (-4+-6)/2= -5 1
x1=3^5
x2=1/3
x^((log1/3 x)+4)=1/243
x^(log1/3 x)*x^4)=1/3^5 лево право больше 0 пролагарифмируем обе части
основание пусть 1/3 будет
log1/3 ( x^(log1/3 x)*x^4)) = log1/3 (1/3^5)
log1/3 ( x^(log1/3 x)) + log 1/3 x^4 = 5
log1/3 x * log1/3 x + 4* log 1/3 x -5=0
log 1/3 x = t
t^2+4t - 5 =0
D=16+20=36
t12= (-4+-6)/2= -5 1
x1=3^5
x2=1/3
Автор ответа:
0
нравица ставь лучший
Автор ответа:
0
ОДЗ
x>0 U x≠1
Логарифмируем обе части уравнения по основанию 1/3
log(1/3)(x^log(1/3)x+4)=log(1/3)(1/243)
(log(1/3)x+4)*log(1/3)x=5
log(1/3)x=a
a²+4a-5=0
a1+a2=-4 U a1*a2=-5
a1=-5⇒log(1/3)x=-5⇒x=243
a2=1⇒log(1/3)x=1⇒⇒⇒x=1/3
Автор ответа:
0
вах красавец решал-решал решал-решал подсмотрел, списал и решил
Автор ответа:
0
Одз x<> 1 можно было тогда и любое число например миллион или 9999 включить нет впанятии логарифма такого по одз
Похожие вопросы
Предмет: История,
автор: samamagulmamedova
Предмет: Математика,
автор: zoskijcel6
Предмет: Русский язык,
автор: nasta17483
Предмет: Литература,
автор: lica01
Предмет: Литература,
автор: Аноним