Question

в треугольник авс вписана окружность которая касается стороны ав в точке м, ab=5 см,bc=7 см,ac=8 см. найдите am

Answer 1

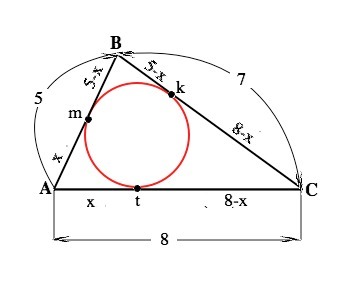
  По теореме о касательных: Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой.  Обозначим  точку касания на ВС k; на АС – t.  Примем Аm=х.  Тогда  Аt=Аm=х; Вm=Вk=5-х, Ck=Ct=8-х. Р∆АВС=5+7+8=20 см. Сумма отрезков сторон равна периметру ∆ АВС. Составим уравнение: 2х+2•(5-х)+2•(8-х)=20 или х+5-х+8-х=10⇒ х=3 см. Аm=х=3 см.