Предмет: Математика,
автор: retardboy
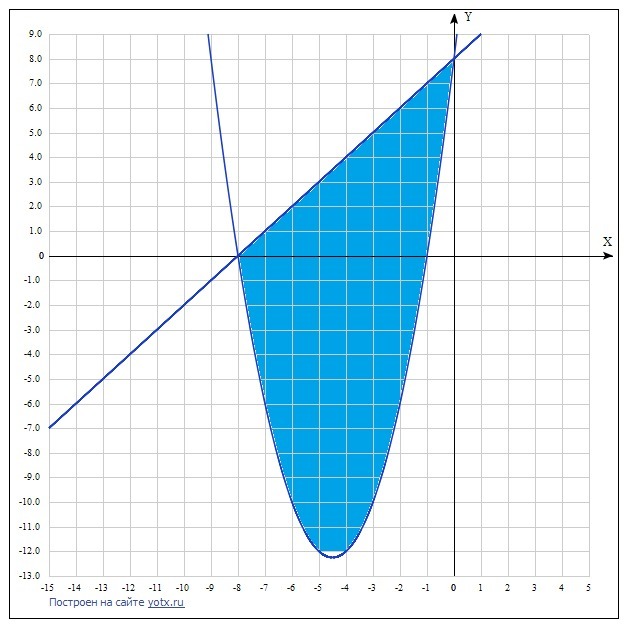
Вычислить площадь фигуры,ограниченной линиями y-x=8 и x^2+9x=y-8
Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: evgenius82
Предмет: Математика,
автор: daidomashky
Предмет: География,
автор: AniaIpatova
Предмет: Математика,
автор: murzikkai