Предмет: Алгебра,
автор: Zanai
38 баллов помогите интеграл
Приложения:
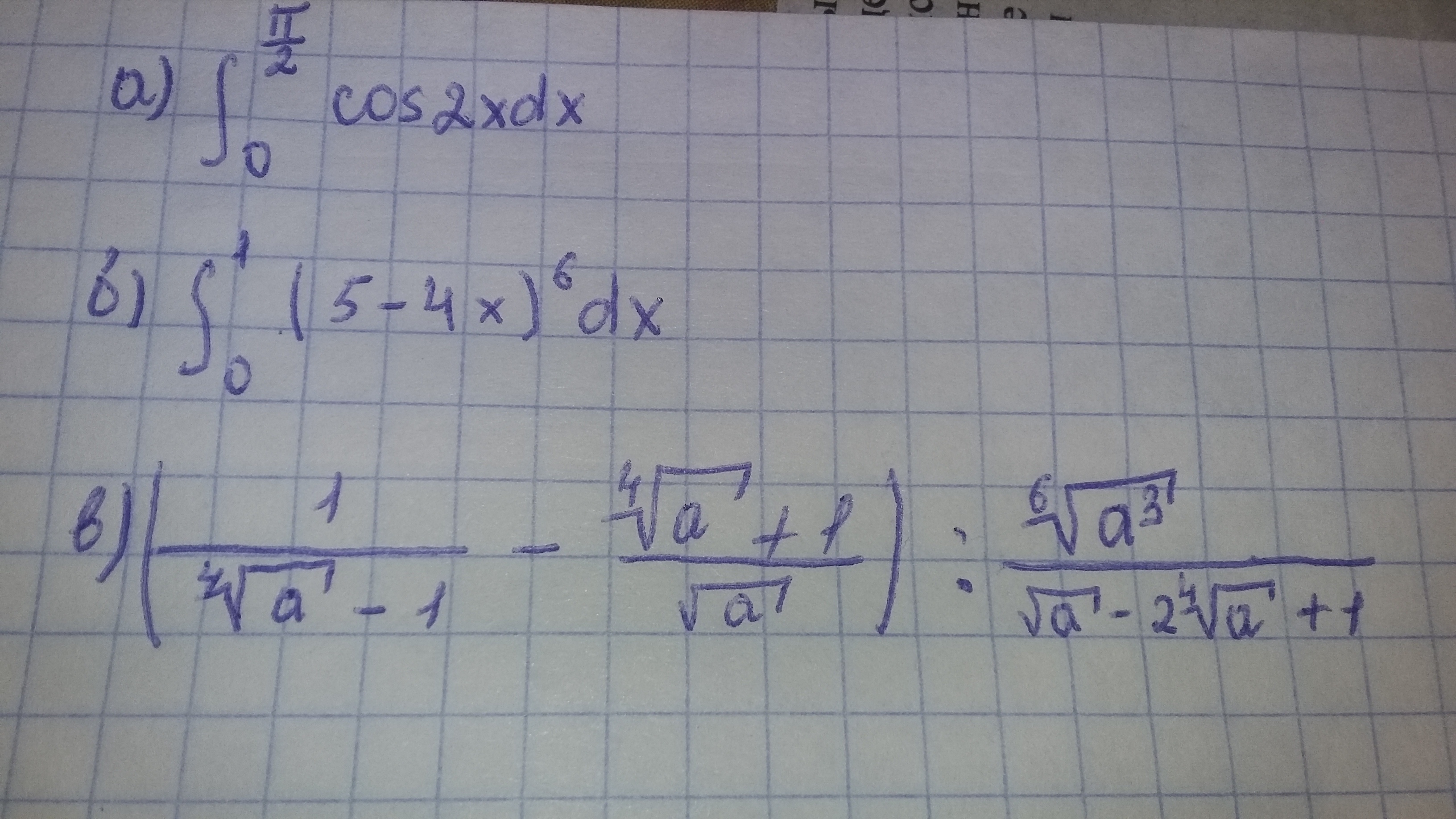
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: sandrarap39719
Предмет: Литература,
автор: milafka69
Предмет: Химия,
автор: francoisrableas228
Предмет: Математика,
автор: beloshaokin03