Предмет: Алгебра,
автор: xcvbnm3
Упростить выражение

Ответы
Автор ответа:
0
Автор ответа:
0
Решение смотри в приложении
Приложения:
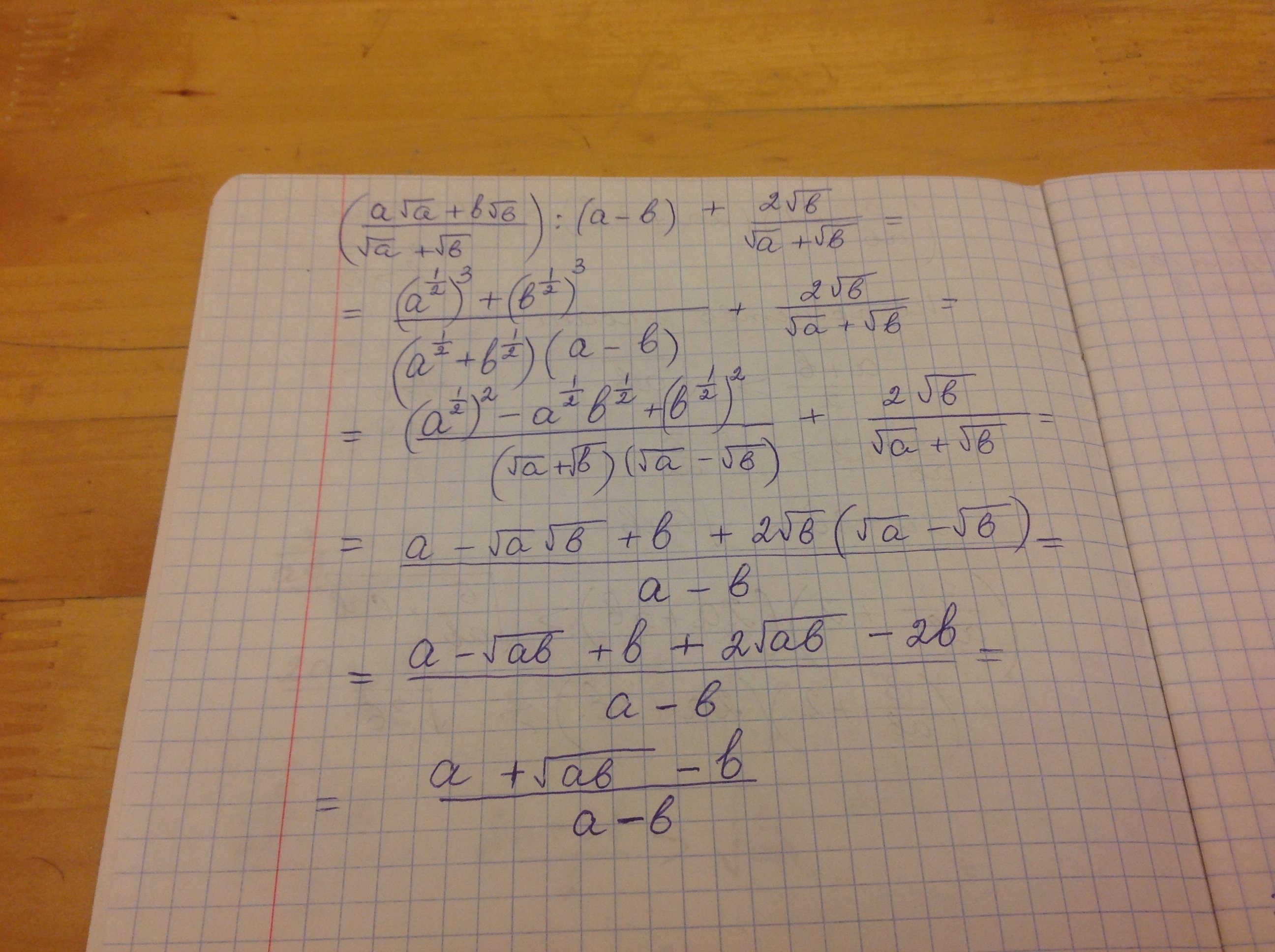
Похожие вопросы
Предмет: Математика,
автор: ajdamirerzan
Предмет: Алгебра,
автор: yarosrudnev
Предмет: История,
автор: dimovanadya2008
Предмет: Химия,
автор: annal2008
Предмет: История,
автор: fedorovaida