Предмет: Алгебра,
автор: fedotycheva99
Большая просьба,решить мне вариант из 5 заданий.
Желательно до вторника,ещё лучше до пн.
С полным решением,желательно сразу все 5 заданий.
Будет отлично,если решение напишите в тетради и пришлёте,чтобы всё было понятно.
Приложения:


Ответы
Автор ответа:
0
Решение во вложении.
Приложения:

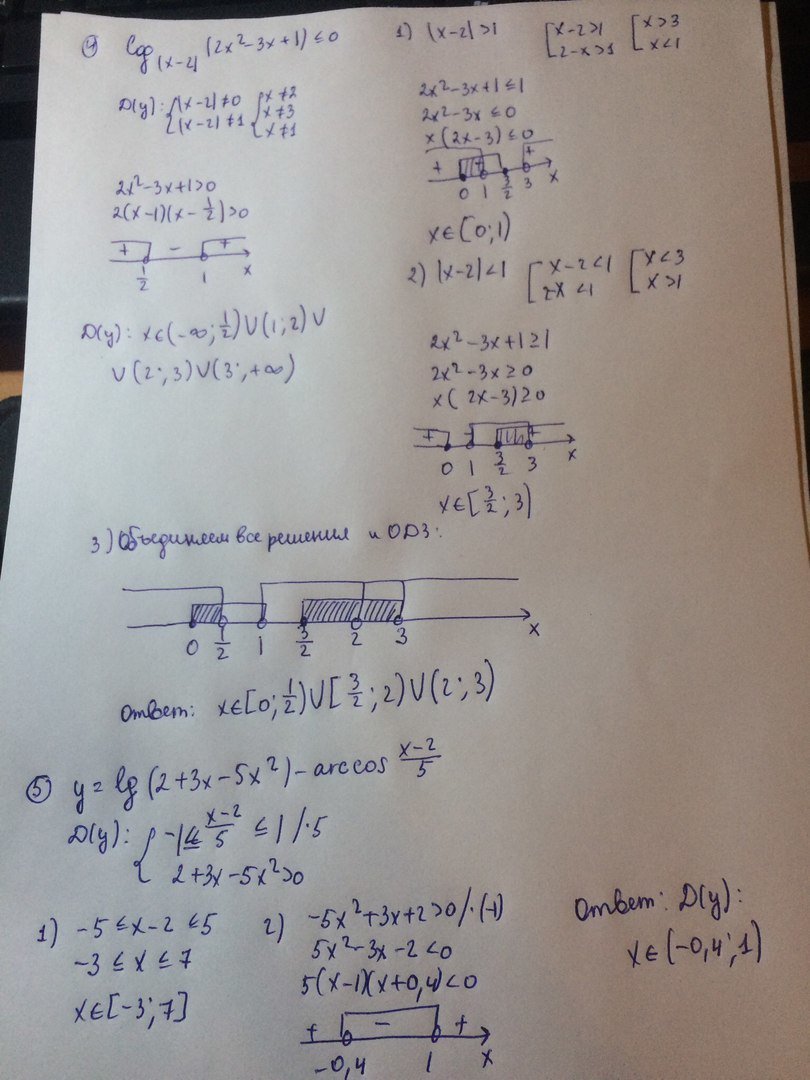
Автор ответа:
0
Откуда эти примеры?
Автор ответа:
0
1
log(2)3*log(2)4/log(2)3=log(2)4=2
2
y=log(2)x
x 1/2 1 2 4 8
y -1 0 1 2 3
y=√√(3-x)
x -1 2 3
y 2 1 0
Ответ x=2
3
ОДЗ
{x+10>0⇒x>-10
{x≠0
x∈(-10;0) U (0;∞)
log(4)(x+10)+log(4)|x|=log(4)24
log(4)[+x|*(x+10)]=log(4)24
|x|*(x+10)=24
1)x∈(-10;0)
-x*(x+10)=24
x²+10x+24=0
x1+x2=-10 U x1*x2=24
x1=-6 U x2=-4
2)x∈(0;∞)
x(x+10)=24
x²+10x-24=0
x1+x2=-10 U x1*x2=-24
x1=2 U x2=-12∉ОДЗ
Ответ x={-6;-4;2}
4
ОДЗ
{|x-2|≠0⇒x-2≠0⇒x≠2
{|x-2|≠1⇒x-2≠-1 U x-2≠1⇒x≠1 U x≠3
{2x²-3x+1>0⇒x<1/2 U x>1
D=9-8=1
x1=(3-1)/4=1/2 U x2=(3+1)/4=1
x∈(-∞;1/2) U (1;2) U (2;3) U (3;∞)
1)x∈(1;2) U (2;3) основание меньше 1
2x²-3x+1≥1
2x²-3x≥0
x(2x-3)≥0
x≤0 U x≥1,5
x∈[1,5;2) U (2;3)
2)x∈(-∞;1/2) U (3;∞) основание больше 1
0≤x≤1,5
x∈[0;1/2) U (1/2;1)
Ответ x∈[0;1/2) U [1,5;2) U (2;3)
5
{-1≤(x-2)/5≤1⇒-5≤x-2≤5⇒ -3≤x≤7
{2+3x-5x²>0⇒5x²-3x-2<0⇒-0,4<x<1
x∈(-0,4;1)
log(2)3*log(2)4/log(2)3=log(2)4=2
2
y=log(2)x
x 1/2 1 2 4 8
y -1 0 1 2 3
y=√√(3-x)
x -1 2 3
y 2 1 0
Ответ x=2
3
ОДЗ
{x+10>0⇒x>-10
{x≠0
x∈(-10;0) U (0;∞)
log(4)(x+10)+log(4)|x|=log(4)24
log(4)[+x|*(x+10)]=log(4)24
|x|*(x+10)=24
1)x∈(-10;0)
-x*(x+10)=24
x²+10x+24=0
x1+x2=-10 U x1*x2=24
x1=-6 U x2=-4
2)x∈(0;∞)
x(x+10)=24
x²+10x-24=0
x1+x2=-10 U x1*x2=-24
x1=2 U x2=-12∉ОДЗ
Ответ x={-6;-4;2}
4
ОДЗ
{|x-2|≠0⇒x-2≠0⇒x≠2
{|x-2|≠1⇒x-2≠-1 U x-2≠1⇒x≠1 U x≠3
{2x²-3x+1>0⇒x<1/2 U x>1
D=9-8=1
x1=(3-1)/4=1/2 U x2=(3+1)/4=1
x∈(-∞;1/2) U (1;2) U (2;3) U (3;∞)
1)x∈(1;2) U (2;3) основание меньше 1
2x²-3x+1≥1
2x²-3x≥0
x(2x-3)≥0
x≤0 U x≥1,5
x∈[1,5;2) U (2;3)
2)x∈(-∞;1/2) U (3;∞) основание больше 1
0≤x≤1,5
x∈[0;1/2) U (1/2;1)
Ответ x∈[0;1/2) U [1,5;2) U (2;3)
5
{-1≤(x-2)/5≤1⇒-5≤x-2≤5⇒ -3≤x≤7
{2+3x-5x²>0⇒5x²-3x-2<0⇒-0,4<x<1
x∈(-0,4;1)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: chingizlevoriginal1
Предмет: Музыка,
автор: evgeniacepurnova61
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: seliadriana