Один из внешних углов прямоугольного треугольника равен 120 градусов. Найдите большую и меньшую сторону треугольника, если их сумма равна 24 см.
Ответы
допусти что угол асд=120градусам
тогда смежный с ним будет 180-120=60 градусам(угол авс)
так как сумма углов в прямоугольном треуголнике,не считая прямого,равна90градусом,то угол вас=30
против большего угла лежит боьшая сторона и против меньшего угла лежит меньшая сторона
против угла в 30 градусов лежит сторона в два раза меньшая гипотенузы
тогда составим уравнение
пусть вс=х,а ас=2х
тогда х+2х=24
3х=24
х=8=вс
ас=8*2=16
ответ:8 и 16
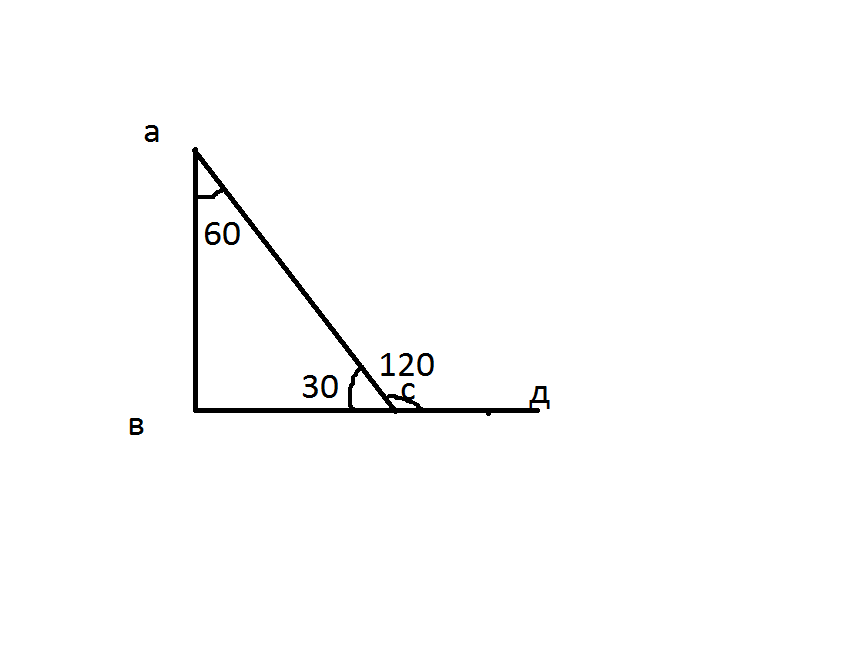
Если внешний угол прямоугольного треугольника 120, то смежный с ним внутренний - 60. Второй острый угол - 30. Большая сторона - гипотенуза. Меньшая сторона - катет, лежащий против угла 30 градусов. А катет, лежащий против угла 30 градусов, равен половине гипотенузы. X+Y=24 X=2Y. Отсюда Y=8, X=16.
Большая сторона - гипотенуза = 16 см. Меньшая сторона - катет = 8 см.
