Предмет: Алгебра,
автор: rrrrtttt01
Пожалуйста помогите........................
Приложения:
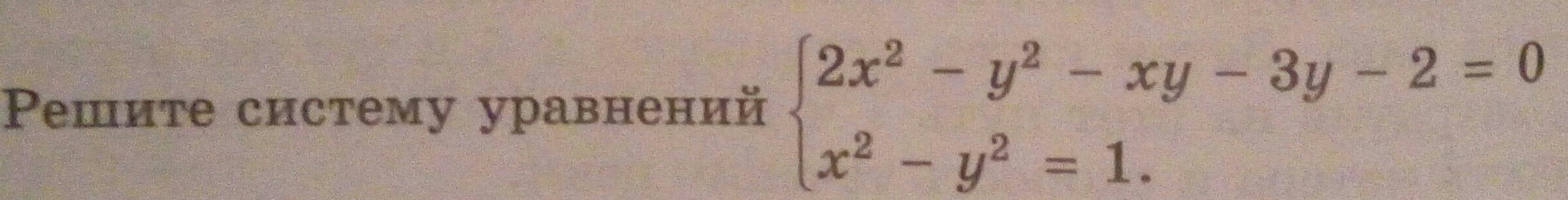
Ответы
Автор ответа:
0
Попробуем разложить левую часть первого уравнения на множители:
Система принимает вид:
Система распадается на две. Решаем первую:
Решаем вторую систему:
Ответ: (1; 0); (-1; 0); (-5/3; 4/3)
Похожие вопросы
Предмет: Английский язык,
автор: Katyku292
Предмет: Математика,
автор: Danya12127
Предмет: Обществознание,
автор: kamilatanikeeva2
Предмет: Алгебра,
автор: elinkamalinka2
Предмет: Математика,
автор: zlata131203