Предмет: Математика,
автор: Oleg09890
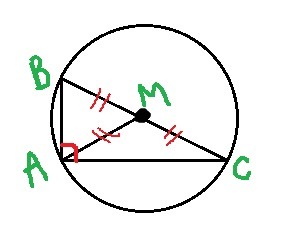
Медиана AM треугольника ABC равна отрезку BM. Докажите, что угол BAC-прямой.
Ответы
Автор ответа:
0
Представим, что точка М - центр окружности, а следовательно отрезки BM, MC и AM равны между собой по условию и равны радиусу данной окружности:
BM=AM=MC=R
получается, что искомый угол BAC опирается на диаметр данной окружности, а мы знаем по теореме, что угол опирающийся на диаметр окружности = 90 градусов
Ч.т.д.
BM=AM=MC=R
получается, что искомый угол BAC опирается на диаметр данной окружности, а мы знаем по теореме, что угол опирающийся на диаметр окружности = 90 градусов
Ч.т.д.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: 87717993728a
Предмет: Физика,
автор: kseniaft87
Предмет: Математика,
автор: saxabievaylia
Предмет: Литература,
автор: kkarishenka2017