Question

Медиана AM треугольника ABC перпендикулярна его биссектрисе BK. Найдите AB, если BC =16
С чертежом, пожалуйста

Answer 1

 обозначим точку пересечения медианы и биссектрисы точкой О  Рассмотрим треугольники АОИ и ВОМ они равны по стороне и двум углам при этой стороне (ВО- общая сторона;  угол АВО равен углу МВО так как ВК биссектриса угла В;  угол АОВ равен углу ВОМ так как АМ перпендикулярна  ВК) Значит АВ равна ВМ, а ВМ=1/2ВС  так как  точка М середина стороны ВС
Значит АВ=1/2 ВС=1/2*16=8

Answer 2

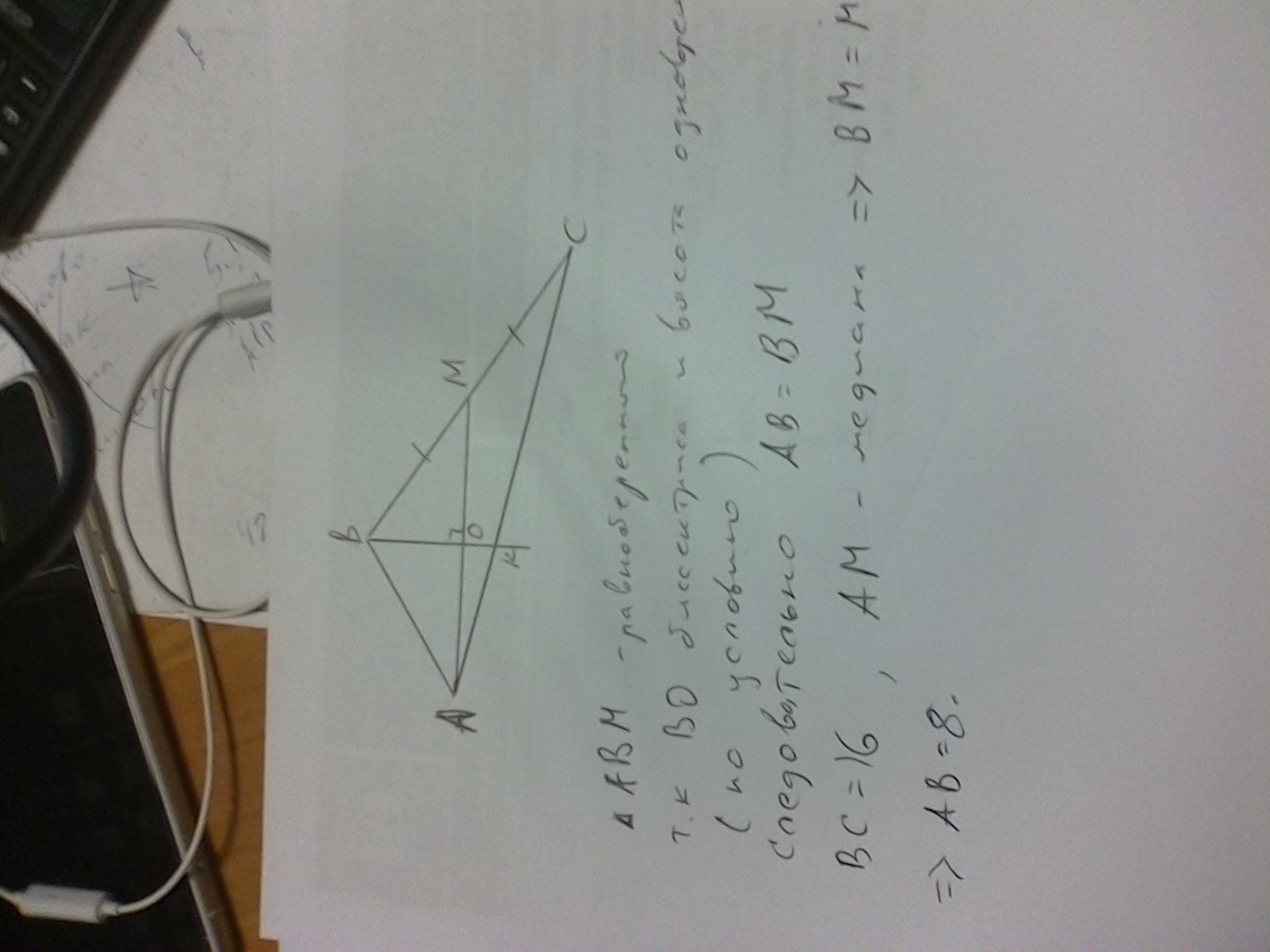
треугольник АВМ равнобедренный, так как ВО является и биссектрисой и высотой одновременно из условия задачи.
ВМ=МС так как АМ медиана и делит сторону ВС пополам, следовательно ВМ=8, следовательно АВ=8 из равнобедренного треугольника АВМ