Предмет: Математика,
автор: anluc98
Найти точку, в которой касательная к кривой
y = 4x - x^2 перпендикулярна к прямой
x - 2y + 6 = 0 . Написать уравнение этой касательной и нормали.
Ответы
Автор ответа:
0
Данная прямая будет иметь вид у=0,5х+3. Ееугловой коэффициент равен к=0,5. Угловой коэффициент перпендикулярной прямой находится к1= - 1/к = -2.
Теперь ищем точку, в которой производная будет равна -2.
y' = 4-2x.
4-2x=-2
x=3. Это точка касания, угловой коэффициент искомой касательной равен -2.
Уравнение касательной составим в виде у-у0 = к*(х-х0)
у0 = у(3) = 4*3-3^2=3.
Уравнение касательной у-3 =-2(х-3); у=-2х+9.
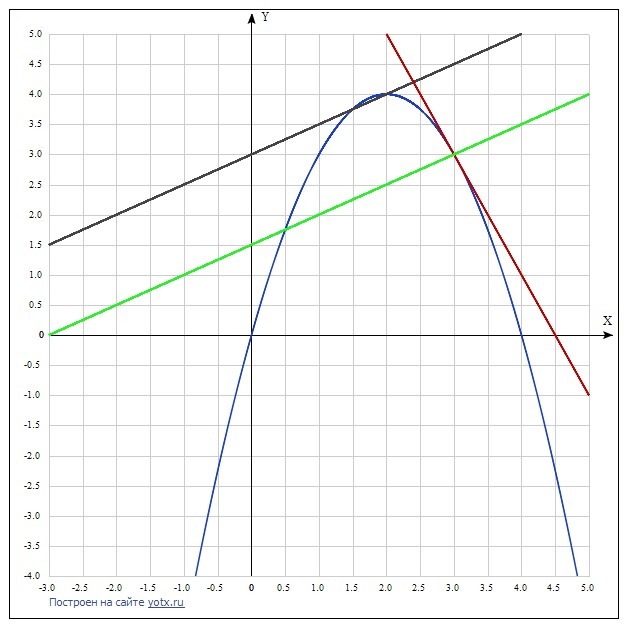
Уравнение нормали у-3 = 0,5(х-3); у=0,5х+1,5. На чертеже данная прямая - черная, касательная - красная, нормаль - зеленая.
Теперь ищем точку, в которой производная будет равна -2.
y' = 4-2x.
4-2x=-2
x=3. Это точка касания, угловой коэффициент искомой касательной равен -2.
Уравнение касательной составим в виде у-у0 = к*(х-х0)
у0 = у(3) = 4*3-3^2=3.
Уравнение касательной у-3 =-2(х-3); у=-2х+9.
Уравнение нормали у-3 = 0,5(х-3); у=0,5х+1,5. На чертеже данная прямая - черная, касательная - красная, нормаль - зеленая.
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: SanTTehNiK
Предмет: История,
автор: mamyshevaq
Предмет: Литература,
автор: aitalinaaf1310
Предмет: Математика,
автор: Uliania20041
Предмет: Литература,
автор: tanyabogodukhova