Предмет: Математика,
автор: hvissa1
Помогите решить 3 и 4 задания!!!!!
Приложения:

Ответы
Автор ответа:
0
4. Так как подстепенное выражение меньше 1, то чем меньше показатель степени, тем больше будет значение выражения. И наоборот - чем больше степень, тем меньше значение. Показатель степени у нас синус. Он может быть равен от -1 до 1. Следовательно, наибольшее значение функция примет при sin x = -1, наименьшее при sin x = 1.
3 - наибольшее значение, 1/3 - наименьшее.
Приложения:
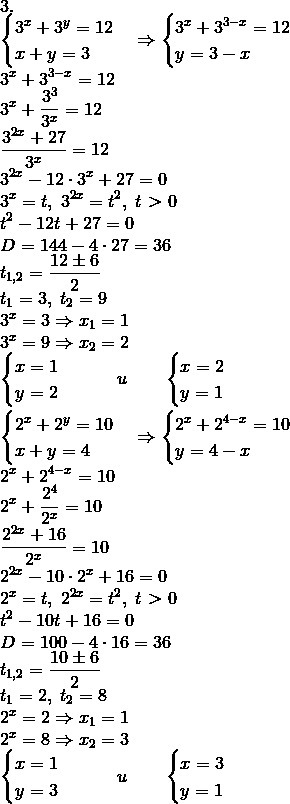
Похожие вопросы
Предмет: Математика,
автор: nogarkov974
Предмет: Математика,
автор: valeriasuspanova67
Предмет: Музыка,
автор: dasaektova747
Предмет: География,
автор: sabrinochka2909
Предмет: Математика,
автор: raisa20066