Предмет: Алгебра,
автор: Аноним
Ответы
Автор ответа:
0
Приложения:
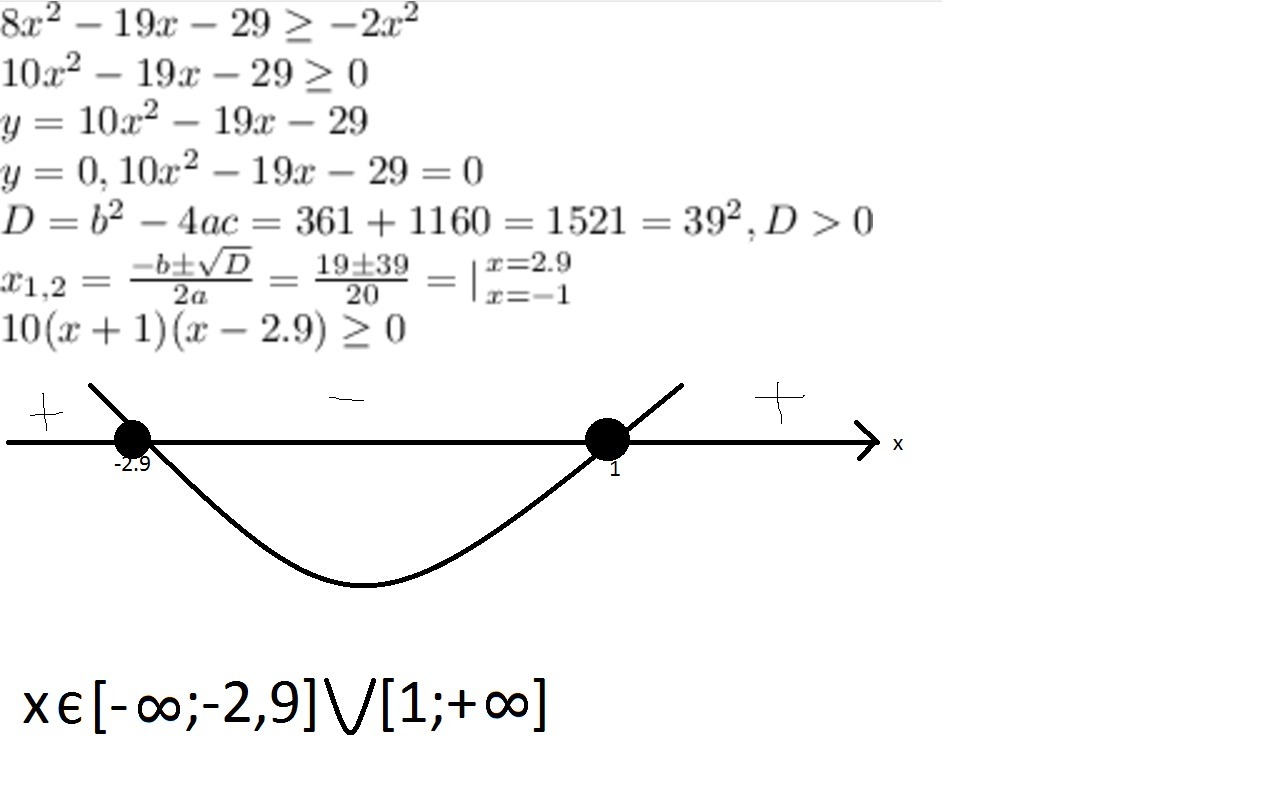
Автор ответа:
0
Приложения:

Похожие вопросы
Предмет: Право,
автор: Pozitiiiv
Предмет: Українська мова,
автор: mm8986467
Предмет: Литература,
автор: arsavskaao8
Предмет: Математика,
автор: diana200425