Предмет: Геометрия,
автор: Аноним
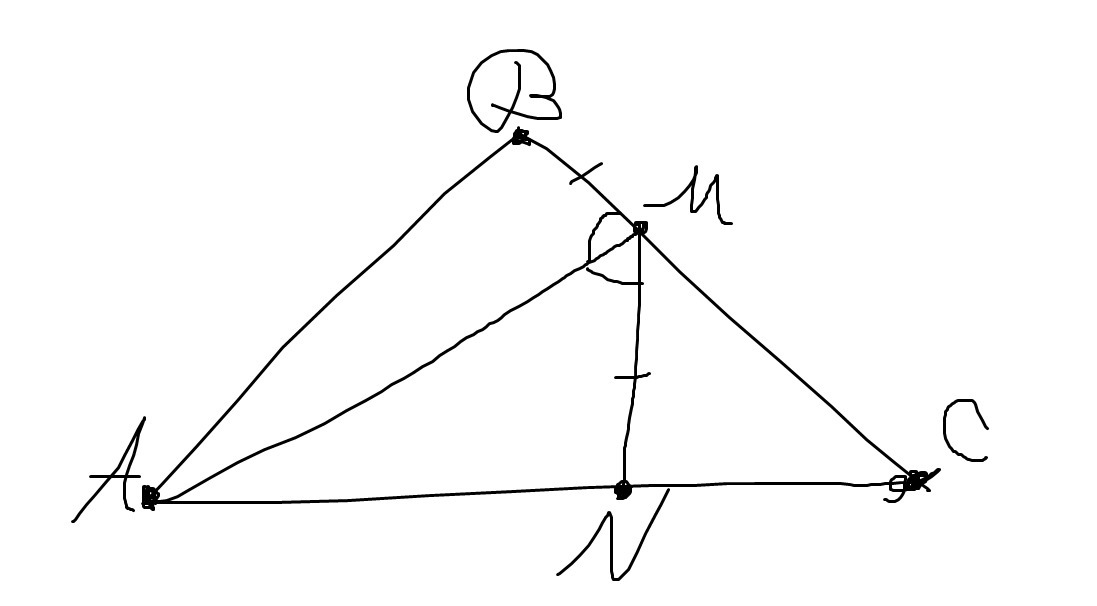
расмотрите рисунок , и докажите что [AM] является биссектрисой треугольника ABC
Приложения:
Ответы
Автор ответа:
0
Рассмотрим ∆ABM и ∆ANM
BM = MN
угол BMA = углу NMA
AM - общая сторона
Значит, ∆ABM = ∆ANM - по I признаку равенства треугольников
Из равенства треугольников => угол BAM = углу MAN => AM - биссектриса, т.к. она делит угол на два рпаныхн между собой угла.
BM = MN
угол BMA = углу NMA
AM - общая сторона
Значит, ∆ABM = ∆ANM - по I признаку равенства треугольников
Из равенства треугольников => угол BAM = углу MAN => AM - биссектриса, т.к. она делит угол на два рпаныхн между собой угла.
Автор ответа:
0
стоп
Автор ответа:
0
[AM] является биссектрисой треугольника ABC
Автор ответа:
0
ключевое
Автор ответа:
0
Тут доказано, что АМ является биссектрисой
Похожие вопросы
Предмет: Математика,
автор: nvenger74
Предмет: Математика,
автор: Skyesx
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: kochetkovasofi