ПОМОГИТЕ ПОЖАЛУЙСТА С ЗАДАЧКОЙ!!!!!1!1!!
В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
Ответы
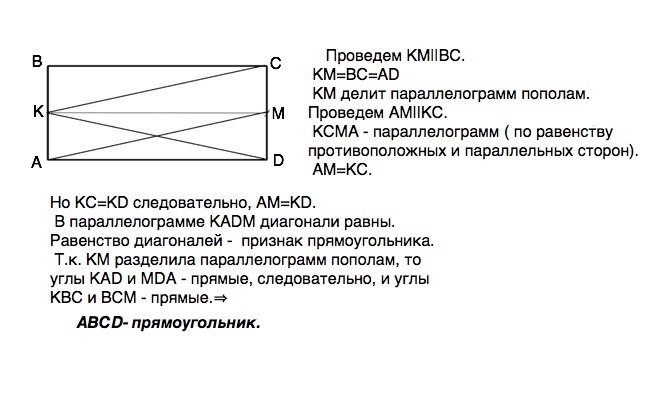
Проведем КМ||ВС. КМ=ВС=АД КМ делит параллелограмм пополам. Проведем АМ||КС. КСМА - параллелограмм ( по равенству противоположных и параллельных сторон).
АМ=КС. Но КС=КD следовательно, АМ=КD.
В параллелограмме КАDМ диагонали равны. Равенство диагоналей - признак прямоугольника.
Т.к. КМ разделила параллелограмм пополам, то углы КАD и МDА - прямые, следовательно, и углы КВС и ВСМ - прямые.⇒
АВСD- прямоугольник.