Предмет: Математика,
автор: guruKotya
Исследовать на сходимость
Приложения:

Ответы
Автор ответа:
0
Автор ответа:
0
Признак Даламбера.


Ряд сходится.
Ряд сходится.
Приложения:
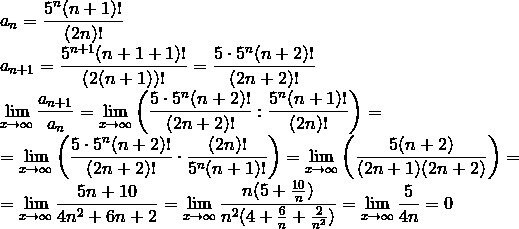
Похожие вопросы
Предмет: Математика,
автор: polina43894
Предмет: Информатика,
автор: vladislavgaryachij03
Предмет: Геометрия,
автор: Bobomarley
Предмет: Химия,
автор: Аноним