Предмет: Алгебра,
автор: XTenagerX
Помогите решить два иррационального уравнения вообще не шарю
Приложения:
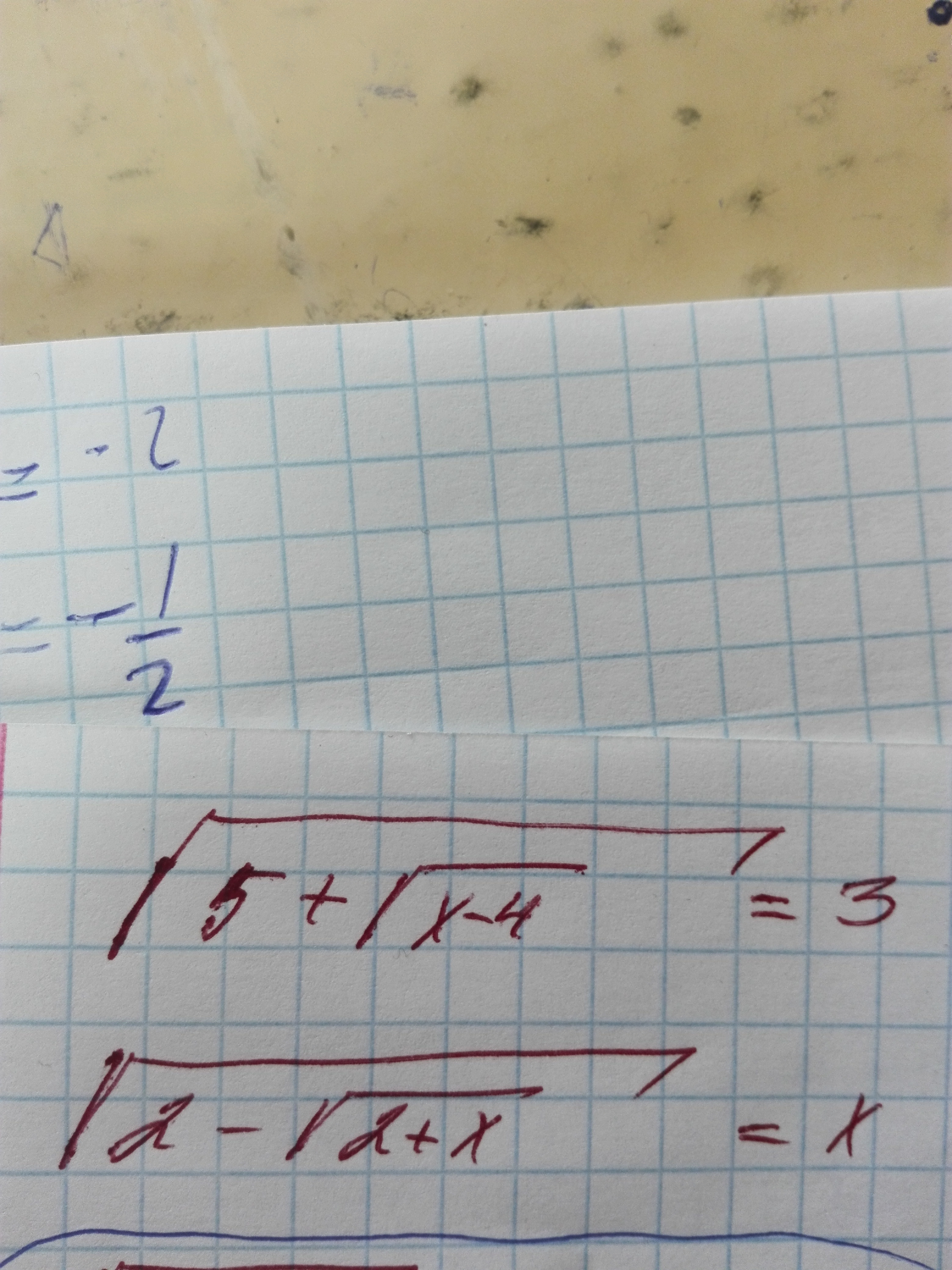
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: yusufsalimov473062
Предмет: Информатика,
автор: ponchik00167
Предмет: История,
автор: indigo22
Предмет: Алгебра,
автор: alinap98
Предмет: Физика,
автор: okloshka