Предмет: Математика,
автор: Arrynnnnn
Разность корней квадратного уравнения x^2+3x+q равна 7 найдите q
Ответы
Автор ответа:
0
По теореме Виета сумма корней кв. уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение свободному члену. Мы знаем разность корней. Найдём их:

Приложения:
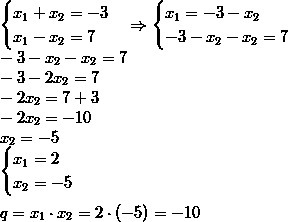
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Физика,
автор: dsisenov62000
Предмет: Музыка,
автор: tabyretka300
Предмет: Физика,
автор: KudAlena2000
Предмет: Информатика,
автор: kostyazakharov1